Проблемът на Königsberg мостове

Позоваването

С благородническа титла "Преброяване" се свързва с темата на моята работа е само общ произход от латинската дума "граф" - пиша.

Брои мен, които се интересуват за способността му да помогне за решаването на различни пъзели. математически и логически задачи. Така че, както се подготвях за олимпиада по математика, теорията на графите е от особено значение в подготовката ми. Реших да разберете каква роля в ежедневния живот се брои за игра.

Целта на

За да се изследва ролята на графиките в живота ни.

Да се ​​научим да работим с програмата за обучение на Microsoft PowerPoint.

Научете как да организираме информацията и създаване на хипервръзки между слайдовете.

Какво е Ърл

Думата "графиката" по математика означава картина, където рисува няколко места, някои от които са свързани с линии. В процеса на решаване на проблемите на математиката забелязах, че е удобно да представлява точка обект. и връзката между двете линии или дъги.

Какво е Ърл

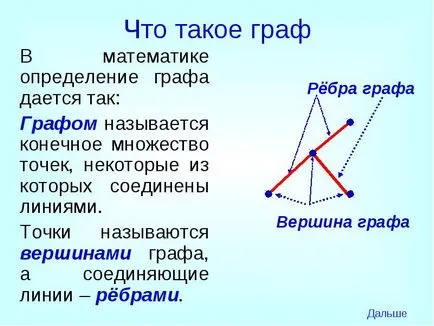
В математиката, дефиницията на графика е даден, както следва:

Броят е крайно множество от точки, някои от които са свързани с линии.

Точките се наричат ​​върхове и свързващи линии - ръбове.

Какво е Ърл

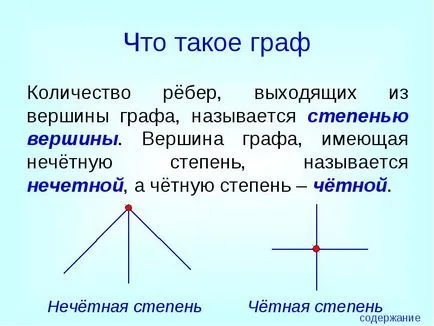
Броят на ръбовете, напускащи връх на графиката, наречена степента на връх. Vertex като странна степен, наречена странно. и chotnuyu степен - дори.

История на наличието графики

Терминът "графиката" се появява за първи път в книгата на унгарския математик Г. Кьониг през 1936 г., въпреки че първоначалните важните теореми на графики датира от Ойлер.

История на наличието графики

Основи на теория на графите като математическа наука положен в 1736, Леонард Ойлер. като се има предвид проблема с Кьонигсберг мостове. Днес, този проблем се превърна в класика.

Проблемът на Кьонигсберг мостове

Бившият Кьонигсберг (сега Калининград), разположен на брега на река Прегел. В рамките на града, реката мие двата острова. На бреговете на острова бяха мост. Старите мостове не са запазени, но имаше карта на града, където са показани.

Проблемът на Кьонигсберг мостове

Kenigsbergtsy предлагат на посетителите следния проблем: да се предаде на всички мостове и да се върнете към началната точка. И на всеки мост само веднъж трябва да посетите.

Проблемът на Кьонигсберг мостове

Разходка на Кьонигсберг мостове, при спазване на дадените условия, не е възможно. Преминаването на всички мостове, при условие, че трябва при всяко посещение, веднъж и да се върнете към началната точка на пътуването, на езика, на теория на графите изглежда като обективен образ "един удар" графика на.

Проблемът на Кьонигсберг мостове

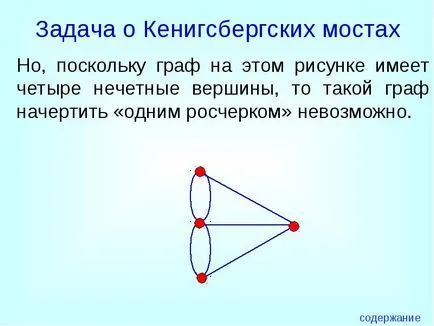
Но, тъй като графиката в тази цифра има четири нечетни върха, след като графика се направи "един удар" е невъзможно.

един удар

Графика, които могат да бъдат изготвени. без повдигане молива от хартията, наречен Ойлер.

Решаването на проблема на мостовете Königsberg, Ойлер формулирани свойствата на графиката:

Невъзможно е да се изготви графика с нечетен нечетен брой върхове.

един удар

Ако всички върхове на странно, можете да без да вдигате молива от хартията ( "един удар") се извършва само веднъж, за да се направи графиката на всеки ръб. Движението може да започне във всеки връх и да го завърши по същия върха.

един удар

Графика като само две нечетни върхове. Това може да се направи, без да вдигате молива от хартията и движението трябва да започне с един от тези странни върхове и финала във втория от тях.

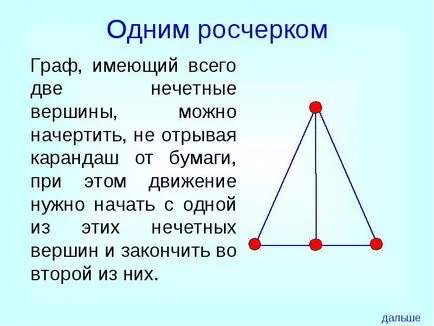
един удар

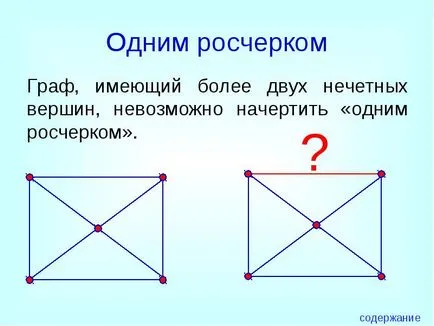
Графика с повече от две нечетни върхове, не е възможно да се направи "един удар".

Използването на графики

С помощта на графики опростени математически решаване на проблеми, пъзели. Tricky задачи.

Използването на графики

Аркадий и Борис. Владимир, Грегъри и Димитри по време на срещата си размениха ръкостискания (всеки се ръкува с всеки един по един). Колко ръкостискания са направени?

Използването на графики

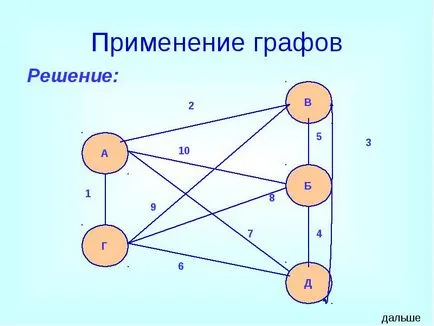
Използването на графики

Лабиринтът - графика. И това проучи - е да се намери път в тази графика.

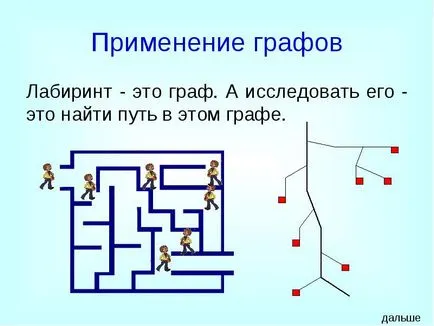
Използването на графики

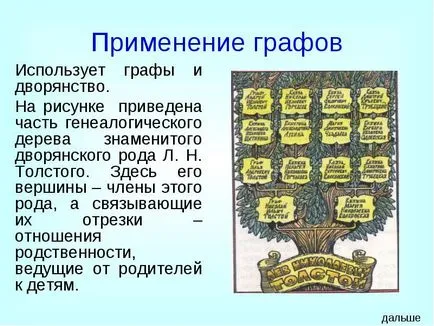
Тя използва графики и благородство.

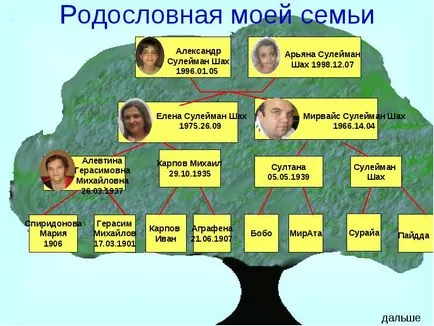
Цифрата показва част от родословното дърво на известния благородно семейство Л. Н. Tolstogo. Тук, чийто връх - членовете на този род, и свързващи сегменти - афинитет отношения водеща от родителите на децата.

Използването на графики

Графит е блок - програмиране схеми за компютри.

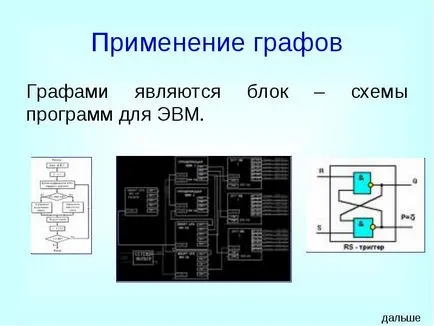
Използването на графики

Графит е мрежата строителните графици.

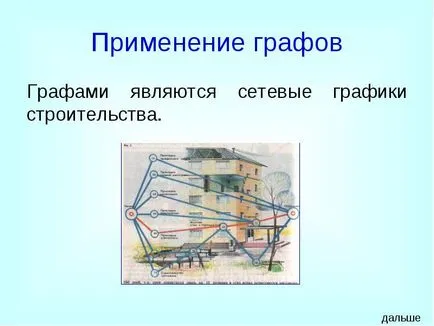
Използването на графики

• Типични графики на карти са образа на железопътния транспорт.

Използването на графики

• Типични графики на картите на града са тенденциите в трафика на градския транспорт.

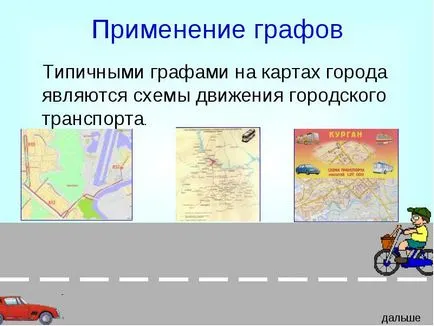
Използването на графики

Типични графики са схеми на авиокомпаниите, които често са публикувани на летищата.

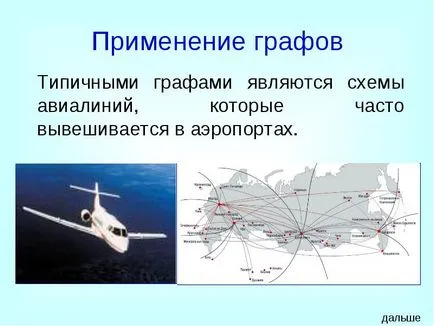
Използването на графики

Използването на графики

Броят е системата на градските улици. Неговите най-добрите - площади и кръстовища, както и от краищата - по улиците.

Използването на графики

Използването на графики

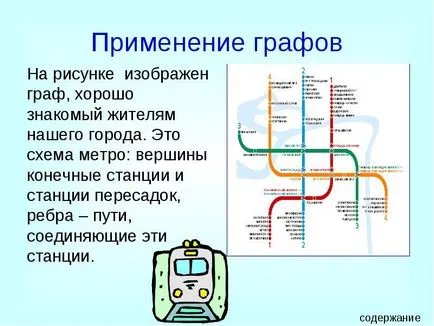
Цифрата показва графика, познат на жителите на нашия град. Това метро схема: най-крайните станции и директни, ребра - маршрути, свързващи тези станции.

Графики - забележителни математически обекти, с помощта на които можете да се реши математически, икономически и логически задачи. Можете също така да решават различни пъзели и да се опростят условията за проблеми във физиката, химията, електрониката и автоматизацията. Графиките се използват при изготвянето на карти и родословни дървета.

В математиката, има дори специална секция, която се нарича "теория на графите".

Позоваването

3.Grafy и тяхното прилагане, О. руда, София, 1979.