Проблеми с практическото съдържание на "подобни триъгълници" платформа съдържание
Задача №1.Nepriyatelskaya кула
Open пътна отсечка, съхранявани на лента с ширина 50 метра AB; враг наблюдателен пост на се намира в горната част на височина камбанария MN = 22м. Какво трябва да направи височина вертикално HF маска на разстояние 500 метра от камбанарията да затвори пътя от наблюдателя на врага?
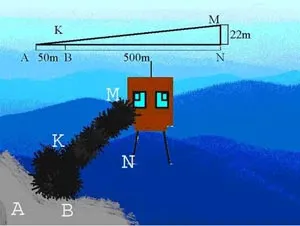
AMN, AB = 50 m,
MN = 22 метра,
BN = 500 метър
AMN (2-ри ъгли: A - Най-общо, AVK и AMN - прави, и ако триъгълници са подобни, тогава всичките му елементи, също са като думи, и по тази причина, м ...
Колко далеч може да се види от балон, който се е повишила до височината на 4 км над Земята (приблизително равно на 6370 km радиус на Земята)?
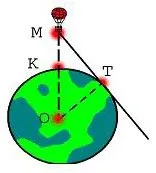
1. Чрез теоремата на допирателната към окръжността, перпендикулярна на допирателната на радиус провежда до точката на контакт, т.е. OTM = 90 °.
2. MO = 4 + 6370 = 6374 km,
3. Тогава питагорова теорема:
MT 2 2 + OT = MO 2
MT 2 = МО 2 - OT 2
MT = 112,9 км
На улицата Pritomskaya-Quay стои 17-етажна сграда, чиято височина е 500 м. Каква е височината на дървото трябва да расте HF, ако човек стои на 2 м. От него, за да затворите пътя и изграждането на наблюдателя? (Разстоянието между дървото и сграда 22 m).
AMN, AB = 2m,
MN = 500м,
BN = 22 метра .Nayti: HF.
А - като цяло, AVK и AMN - прав
AMN (2-м ъгли),
Това вижда мъж, който стоеше на покрива на хотел Crystal на това, ако на другия човек, който е 1.8 m височина, стои на разстояние от 1.83 m от другите сгради. Ако можете да го наричат сградата. (Хотелска сграда Crystal 500 m).
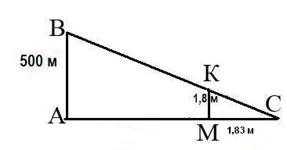
MCS (т-2 ъгли)
A: Необходимата сградата SEC "Лапландия".
Елбрус (Кавказ) се издига над морското равнище до 5600 m. Колко далеч може да се види от върха на тази планина?
М - наблюдение след височина Н метра един над земята; Земята радиус R, MT = г е най-големият видимо разстояние. Докажете, че.
Най-горе в планината може да се види от точка А под ъгъл от 38 на 42 "и подхода към планината до върха на 200 метра се вижда под ъгъл от 42. Намерете височината на планината.
Задачата на китайците "Математика в девет книги"
"Има езерце със страна 1 = Чанг 10 чи. В центъра нараства тръстика, която се издава над водата в една чи. Ако дръпнете тръстиката до брега, той просто се докосне. Въпросът е: каква е дълбочината на водата, и това, което е дължината на пръчката ".
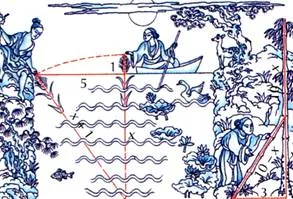
Задачата на учебника "Аритметика" Leontiya Magnitskogo.
"Няма един човек се е случило с pribrati стената стълба, височина на стената на играчката разполага със 117 фута. И да обръсне, стълбищните дължина 125 фута. И Ведат иска, колики спиране причинява долния край на стълбата от стената otstoyati има. "
Tree измерване на височината.
За да се измери височината на дърво BD, изготвен AV1C1 правоъгълен триъгълник с ъгъл А = 45 °, и, като го държите вертикално, се премества на разстояние, на което, гледайки заедно хипотенузата на АВ 1, видя на върха на дърво B. един Каква е височината на дървото, ако разстоянието
AC = 5,6m и височина 1,7 м на лицето?
AV1S1,
= 90 ° С,
А = 45 градуса.
AC = 5,6m
Н = 1.7m човек.
1), тъй като е обща за двете триъгълници и AS1V1 и DIA (от хипотеза) директно (т.е., равно на 90 °), след това AS1V1 и DIA - като (на базата на сходство на 2 ъглите).
2) След това AV1C1 = ABC = 45 °, => BC = AC = 5,6m, но за да получите дължината, ние трябва да се прибави височината, т.е. дължината на дърво DB = 7,3m.