Примери за използване на цилиндрични и сферични координати

Както и при прехода към полярни координати в двоен интеграл, даде еднозначен рецепта за кога да се използват цилиндрични или сферични координати, ние не можем, това е въпрос на опит. Можете да се опитате да използвате цилиндрични координати, ако подинтегрален и / или уравнения на повърхностите, които ограничават размера на $ \ mathbf> $, в зависимост от комбинацията от $ \ mathbf> ^ + \ mathbf> ^ = \ mathbf> ^<2>$; сферична - ако тези уравнения зависят от $ \ mathbf> ^ + \ mathbf> ^ + \ mathbf> ^ = \ mathbf> ^<2>$. Помислете за някои примери.

Намерете сумата от $ \ mathbf> $ общата сума на две топки, зони с ограничен достъп

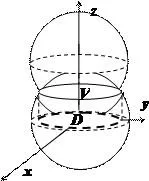
Пресечната точка на сферите се намира в $ 2Rz = R ^ 2 \ стрелкаНадясно Z = R / 2 и $ е окръжност с радиус R $ \ Frac $. Обемът на $ \ mathbf> $ е ограничена отгоре от повърхността $ Z = \ SQRT $, по-долу - повърхността $ Z = R- \ SQRT $. Изчисленията в декартови координати дадени $ V = \ iiint \ limits_V = \ iiint \ limits_V = \ Int \ граници _> ^> R ^ 2-х ^ 2 >> ^ R ^ 2-х ^ 2 $ >>> >>> ^ - доста тежки изчисления.

В цилиндрична координира размер на $ \ mathbf> $ е ограничена отгоре от повърхността $ Z = \ SQRT $, по-долу - повърхността $ Z = R- \ SQRT $, така че

В сферични координати, сфера уравнение дъното става $ R = R $, най - $ R ^ = 2RR \ защото \ тета \ стрелкаНадясно г = 2R \ 2 защото \ тета $, тяхното пресичане съответства на стойност $ \ защото \ тета = 1/2 \ стрелкаНадясно \ тета = \ пи / 3 $. В диапазона от 0 $ \ leqslant \ тета \ leqslant \ пи / 3 \ четири \ mathbf> $ варира от $ 0 $ до $ \ mathbf> $, в диапазона от $ \ пи / 3 \ leqslant \ тета \ leqslant \ пи / 2 \ четири \ mathbf> $ варира от $ 0 $ $ да 2R \ защото \ тета $, така че

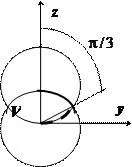
В този пример, сложността на изчисленията в цилиндрични координати и сферични за същото.

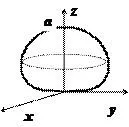
Изчислява се обема на тялото, ограничена от повърхността $ \ ляво (\ дясно) ^ = ^ а 3Z, \; а = конст> 0 $

Изчислете неразделна $ \ iiint \ limits_U + 2 +> \ дясно) dxdydz> $ където региона (U) е ограничено от повърхността (+ \ ле 1) и равнината (Z = 0,) (Z = 1).

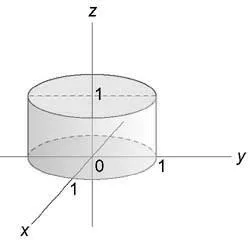
Това е удобно, за да се изчисли интеграла в цилиндрични координати. Зоната за проекция на интеграция на самолета (окси) е кръг (+ \ ле 1) или (0 \ ле \ р \ ле 1).

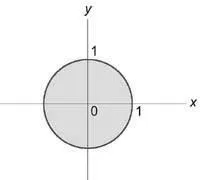
Тогава интеграл е равно на $ I = \ Int \ limits_0 ^ \ Int \ limits_0 ^ 1 \ р г \ р> \ Int \ limits_0 ^ 1. $

Тук, във втората съставна добавя фактор (\ р) Jacobian на преобразуването на декартови координати в цилиндрична. И трите интеграла за всяка променлива са независими една от друга.

Изчислете интегрални $ \ iiint \ limits_U +> \ дясно) dxdydz>, където $ региона (U), ограничена от повърхностите (+ = 3Z,) (Z = 3)

интеграция площ е изобразена на фигура

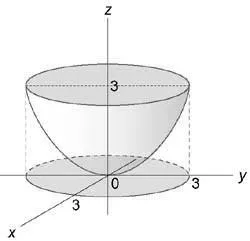
За да се изчисли неразделна завой към цилиндрични координати: $ \; \; \; \; Така $ Диференциална равнява $ dxdydz = \ р г \ р г \ varphi DZ \; \; \ наляво (> \ дясно) $.

Уравнение параболична повърхност е под формата: $ \ varphi + \ varphi = 3z \; \; \ текст \; \; = 3Z. $ Проекция интеграция област (U) на равнината (окси) е кръг (+ \ ле 9) радиус (\ р = 3).

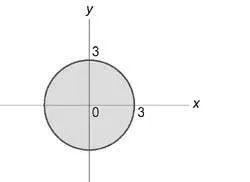
Координатната (\ Rho) варира от (0) до (3), че ъгълът (\ varphi) от (0) до (2 \ пи) и координатната (Z) на (\ голям \ Frac >> \ normalsize) до ( 3.)

Използването на цилиндрични координати, намерете стойността на интегралната $ I = \ вътр \ limits_<- 2>^ 2 \ вътр \ limits_<- \sqrt>> ^ >> \ вътр \ limits_0 ^ -> DZ> $

Интеграция област (U) е показано по-долу:

Неговата проекция на самолета (окси) е кръг (+ =):

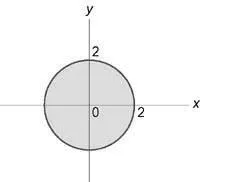
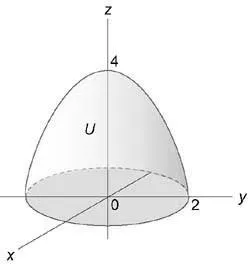
Изчислете неразделна използване на цилиндрични координати: $ \ iiint \ limits_U +> dxdydz> $ пространство (U) е ограничена от параболоид (Z = 4 - -,) цилиндър (+ = 4) и равнините (у = 0,) (Z = 0. )

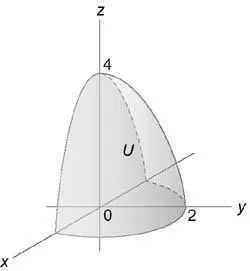
Изобразяване схематично участък интеграция (U,), ние откриваме, че неговата издатина върху равнина (окси) е радиусът на полукръга (\ р = 2).

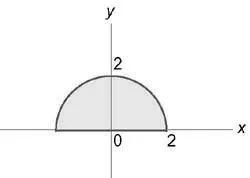
Виж интегрални $ \ iiint \ limits_U, $ където региона (U) е ограничена от равнини (Z = X + 1) (Z = 0) и цилиндрични повърхности (+ = 1) (= + 4)

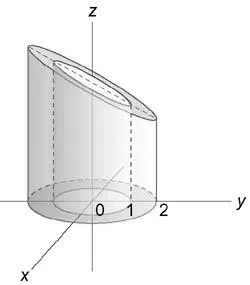
Изчисляваме интеграла в цилиндрични координати. От състоянието на $ 0 \ ле Z \ ле х + 1 $, че $ 0 \ ле Z \ ле \ р \ защото \ varphi + 1. $ диапазон на интеграция в равнината (окси) е анулус ограничена от кръгове (+ = 1) и (= + 4)

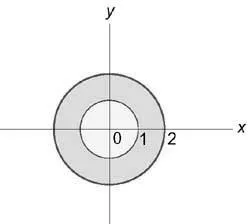
Следователно, променливи (\ Rho) и (\ varphi) варират в границите от 1 $ \ ле \ р \ ле 2 \, \ 0 \ ле \ varphi \ ле 2 \ пи $.

Този резултат е логично от региона (U) е симетрична спрямо равнина (Oxz,) и функцията подинтегрален е дори.

Намерете неразделна (\ iiint \ limits_U + +> dxdydz>), където в района на интеграция (U) топка, дадена от уравнение (+> = 25)

Тъй региона (U) е кръгла, а също подинтегрален е функция, която зависи $ е \ ляво на (+ +> \ полето), $ след това преминава към сферични координати.

Изчислете неразделна $ \ iiint \ limits_U + +> \ дясно)> ^ >>>> dxdydz> $ където региона (U) е единица топка (+ +> \ ле 1.)

В центъра на сферата се намира в основата. Ето защо, в сферични координати, регион интеграция (U) описва неравенството $ \; \; \; \; $

Изчислете интеграл (\ iiint \ limits_U,) където региона (U) е част на топката (+ + \ ле,), разположен в първата ъгломер (х \ GE 0, у \ GE 0, Z \ GE 0.)

Изчислете неразделна $ \ INT \ limits_0 ^ 1 \ вътр \ limits_0 ^ >> \ вътр \ limits_0 ^ - >> + +> \ дясно)> ^ 2> DZ> $ използване сферични координати.

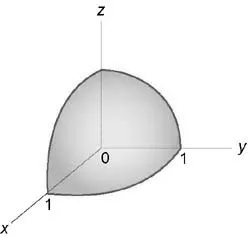
интеграция на района е част от играта, разположен в първия ъгломер и следователно ограничени неравенства $ \; \; > \; \; .> $

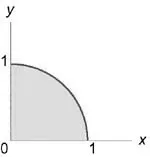
Вижте също:

Изчисляване на площ

Клас $ S $. Теорема на zamknytosti клас $ S $

Имоти тройни неразделна

Клас М. теоремата на клас М е затворен

Напред към съдържанието на $ \ стрелкаНадясно \ стрелкаНадясно \ стрелкаНадясно $