Пример заговор функции, определени по подразбиране

Помислете за заговор функции в следния пример:

Пример. Postroimt графика на \ (х \ на у (х) \), посочено безусловно, параметър schetaete положителен \ (а> 0 \). $$ х ^ 4 + у ^ 4 = а ^ 2 (х ^ 2 + Y ^ 2) $$
Решение. Изследването на функция графика и изграждане си Keypoint. Очевидно е, че графиката на функцията е симетрична спрямо координатните оси, т.е. ще има да извършва изследвания график през първото тримесечие, т.е. в (GEQ 0 \ у \) \ (х \ GEQ 0 \) и \. Функцията се определя и непрекъснато за всички \ (х \). Представлява кривата в параметрична форма, замени \ (у = TX \). защото Нека разгледаме кривата в първата chetveti, а след това \ (у \ GEQ 0 \). Заместването на 4 $$ х ^ + у ^ 4 = а ^ 2 (х ^ 2 + Y ^ 2) => х ^ 4 + (Тексас) ^ 4 = а ^ 2 (х ^ 2 + (Тексас) ^ 2) = > $$$$ х ^ 2 + т ^ 4x ^ 2 = а ^ 2 (1 + т ^ 2) => х ^ 2 = а ^ 2 \ Frac<1+ t^4> = X = а \ SQRT<\frac<1+ t^4>> $$ заменен уравнението за \ (у \) $$ у = TX => у = т а \ SQRT<\frac<1+ t^4>> $$ изчислителни производни \ (х '\) и \ (у' \) $$ х '= (а \ SQRT<\frac<1+ t^4>>) '= \ Frac \ SQRT> \ Frac' = а \ SQRT> \ Frac $$ равнява на първата производна на 0, и да намерят стационарни точки $$ X '= а \ SQRT> \ Frac = 0 => т (1 - 2т 2 ^ -t ^ 4) = 0 => t_1 = 0, t_2 = \ SQRT $$ определяне на знака на производно в околните тези точки, получаваме

получават, в точка \ (т = \ SQRT х = а \ Frac; у = а \ SQRT> \) деривати промени знак + към - т.е. Тази точка на максимална
необходимо да се определи точката на пресичане с оста \ (у \), с ос \ (х \) вече има - крайно. \ (X = 0, х ^ 4 + у ^ 4 = а ^ 2 (х ^ 2 + Y ^ 2) => у ^ 4 = ^ на 2у ^ 2 => у = а \)

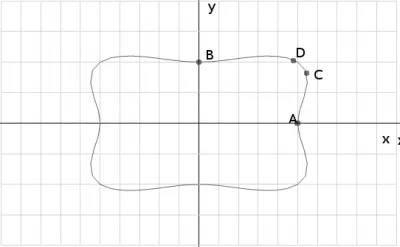
Нанесете точка на декартови координати система, изграждане на крива в първия chetvetri, а след това на картата симетрично по отношение на ос \ (Ox \), а след това \ (Oy \) и се получи следното reschultat