Представяне на синус, косинус и тангенс на ъгъла, получен учител по математика от средното училище 30 име

1 Sine, косинус и тангенс на ъгъл Изготвен: математика учител № 30 на име A.I.Koldunova Kutomanova EM академична година

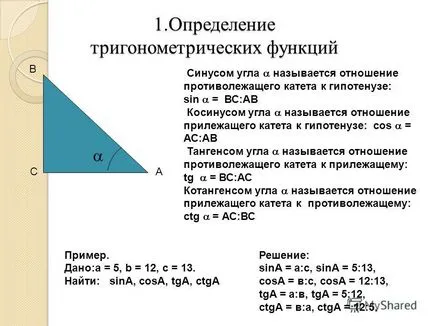
2 1. Определяне на тригонометрични синусова функция на ъгъла е съотношението на другия крак на хипотенузата: грях = VS: AB косинус на ъгъла е съотношението на хипотенузата на съседната страна: COS = AS: AB ъгъл допирателна е съотношението на срещуположната част на крака към съседен: TG = VS: AU ъгъл котангенс Това е съотношението на съседна страна на противоположния: CTG = AC: ВС Пример. Като се има предвид: а = 5, б = 12, с = 13. търсене: Sina, Коза, TGA, ctgA Решение: SINA = а: С, Сина = 5:13, Коза = а: С, Коза = 12:13, TGA = а:, TGA = 5:12, ctgA = а:, ctgA = 12: 5. AC B

3 2.Sinus, косинус, тангенс Въвеждане на правоъгълната координатна система Oxy. Construct полукръг центрирана в произхода и радиус, равен на 1. Това ще се нарича устройството полукръг полукръг. α ъгъл часа между гредата и положителния половината оста Ox. От ΔOMD правоъгълна има: sinα = MD: OM sosα = OD: OM. защото ОМ = 1, у = MD, OD = х, след това sinα = Y, X = sosα. Извършване на C (0; 1) з N (х, у) М (х, у) В (1; 0) 0 α Г (1, 0) х

4 Така, синуса е равен на ъгъл а острите на ординатата на точка М, и косинус на ъгъл а - абсциса точка М. Ако ъгълът α права, тъп или неопакован α = 0 °, синус, косинус на ъгъла а също така определя от формула sinα на = Y sosα = х. Т.е. 0 sinα1, -1 sosα1. Забележка: sin0 ° = 0, sin90 ° = 1, sin180 ° = 0, sos0 ° = 1, sos90 ° = 0, sos180 ° = 1.

5 допирателната ъгълът а е коефициент sinα да sosα, t.e.tgα = sinα: sosα. Когато а = 90 ° не tgα определени, тъй sos90 ° = 0. защото sin0 ° = 0 и sos0 ° = 1, Тд 0 ° = 0. защото sin180 ° = 0 и sos180 ° = 1, Тд 180 ° = 0

6 котангенс на ъгъл а е коефициент sosα да sinα, t.e.stgα = sosα: sinα. Когато а = 0 ° не stgα определени, тъй sin0 ° = 0. Когато а = 180 ° не stgα определени, тъй sin180 ° = 0.

7 3.BASIC тригонометрични звено идентичност DIA полукръг с център О е дъга от окръжност, която има формата на уравнение h² + u² = 1. Извършване на 1012 (за точките М и М). защото sinα = Y, X = sosα след грях ² α + защото ² α = 1. Това равенство е изпълнено за всяко α, 0 ° α180 °. грях ² α + защото ² α = 1 - Питагоровата тригонометрични идентичност Извършване 1013a, 1014a, 1015a.

8 4.Formuly привеждане следните идентичности: при 0 ° α90 ° грях (90 ° -α) = COS α, COS (90 ° -α) = sinα, TG (90 ° -α) = stgα; при 0 ° α180 ° грях (180 ° -α) = sinα, COS (180 ° -α) = -sosα, TG (180 ° -α) = - tgα. Извършване на 1016.

9 Сграда ъгъл, ако знаете, че тригонометрични функции на ъгъла. 1.Postroim ъгъл α, когато грях α = 0,25. Строителство: 1) координатната система Oxy ще изгради звено полукръг с център в основата. 2) Draw права линия у = 0,25. 3) Директна преминава полукръг в точките М и Р 4) изготвя греди ОП и ОМ. Ъглите на ЗНП и АНС - неизвестното. Проблемът има две решения. гг MR OAh

10 2.Postroim ъгъл α, ако COS α = 0,25. Строителство: 1) координатната система Oxy ще изгради звено полукръг с център в основата. 2) Draw права линия х = 0,25. 3) Директна преминава в М полукръг. 4) При равен лъч ОМ. Вие - ъгъл АНС. Проблемът има единствено решение. YM OAh

11 2.Postroim ъгъл α, ако COS α = -0,5. Строителство: 1) координатната система Oxy ще изгради звено полукръг с център в основата. 2) Draw права линия х = -0.5. 3) Директна преминава в М полукръг. 4) При равен лъч ОМ. Вие - ъгъл АНС. Проблемът има единствено решение. в М OAh

Формула 12 за изчисляване на координатите на точка Нека А (х, у), Y0. M (sosα, sinα) - OA лъч пресечната точка и положителния половин Ox, α - ъгъл между линията ОА и положителния половината оста Ox. OA вектор има координати, вектора от -. След х = OA sosα имат OA = sinα. Извършва 1018 (г, г), 1019 (а) XO у А (х, у) А (х, у) М (ф sα, sinα)

Независим работа 13 1 Опция 2 изпълнение Построява ъгъл А, ако 1) Сина = 3/51) Сина = 2/5 2) Sosa = 3/42) Sosa = -3/4 3) Sosa = -2/33) = 2 Sosa / Юли 1018 (а) 1018 (б) домашните §1, претенция 95, 1017 1018 (а) 1019 (б)