Построява се графика скица, знаейки, че - представяне 17823-15

изпълнение на извадката >>

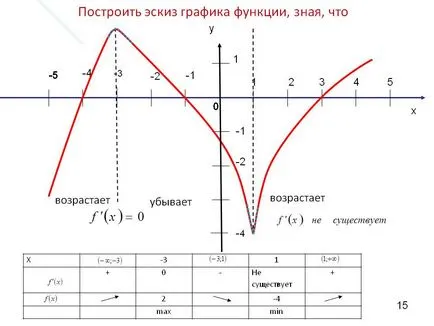
Построява се скица на графиката на знаейки, че. Се увеличава. Се увеличава. Намалява. у. 1. -4. -1. -2. 1. 2. 3. 4. 5. х. -1. -2. -3. -4. -5. 0. 15.

Плъзнете 15 от презентацията, "Използването на производната на изследването на функции", уроците на алгебра на "производни"

Размер: 960 х 720 пиксела, на формат: JPG. За да изтеглите слайда за използване в клас алгебра, щракнете с дясното изображение бутон на мишката и натиснете бутона "Съхраняване изображението като. ". Изтеглете цялата презентация на тема "Приложение на производната на funktsiy.pptx на проучване" може да бъде в цип архив размер на 1 207 KB.

дериват

"Предизвикателства за производно» - F (х) = F (х) - F (x0). x0 x0 +? х. И как си представяте, че моментната скорост? Проблемът на моментния скорост. у. Как си представяте моментната скорост. X = X-x0. Казаното по-горе в писмена форма. На първо място, ние определяме на "територията" на своите изследвания. А л г т р и м. Скорост V на постепенно се увеличава.

"Изследване на производно" - пистолет стреля под ъгъл спрямо хоризонта. Вариант 1 Вариант 2 C D Б Б. МР Meshkovskaya средното училище математика учител Tatiana Kovaleva Функция определя на интервала [-4, 4]. Как са производната на функцията? Отговори: Използване на изследване на функцията за увеличаване и намаляване на функцията. ПРОБЛЕМ забравяйте историята за Барон Мюнхаузен?

"Производно на съставна функция" - сложни функции. Намирането на правилния производно на съставна функция. Производни на прости функции. Производното на съставна функция. Комплекс функция: Примери:

"Урок на производното на съставна функция" - производно на съставна функция. Изчислете скоростта на точка а) по време на тон; б) по време Т = 2 C. Намерете производните на функциите. Ако. Брук Тейлор. Намерете разлика от функцията: За какви стойности на х, равенството. Точка движи праволинейно по право и (т) = S (T) = (а - разстояние в метри, т - времето в секунди).

"Определението на производно" - 1. Доказателство: (? Х + х) е. Нека ф (х). о (х) и w (X) - диференцират в определен интервал (а, б) функция, С - постоянна. е (х). Уравнението на линията на наклона: Чрез Тригонометрия, ние имаме: теорема. След това: Производно на съставна функция.

Като цяло, за "производни" 31 презентация