Площта на плоска фигура в полярни координати изчисляване на обеми на тела - решаването на проблеми, свързани с контрола

Square плоска форма в полярни координати Изчисляване на обема на органите

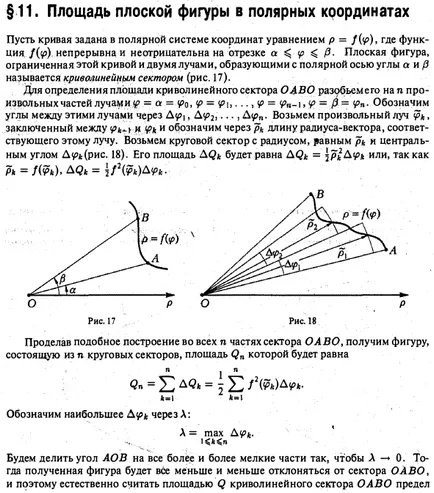
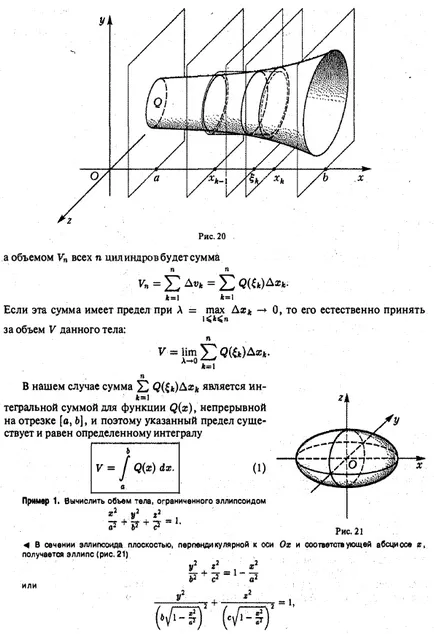
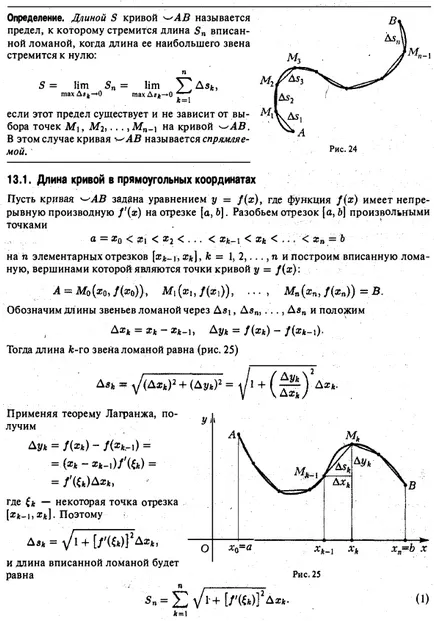
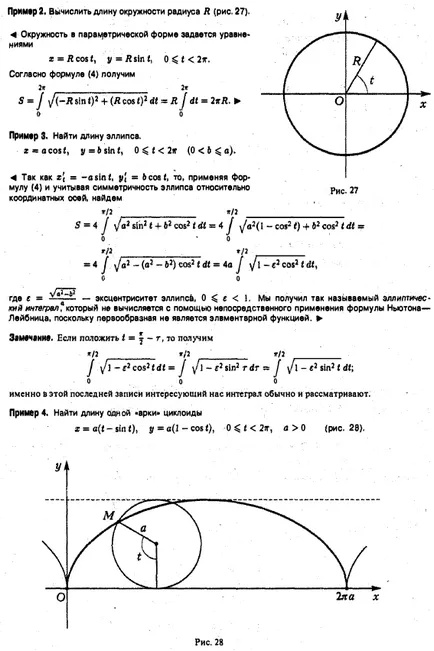
Нека кривата се определя по уравнението в полярна координатна система. където функцията е непрекъсната и неотрицателно на интервала. А равнина фигура ограничена от тази крива и двете греди, образуващи с полярен оста на ъглите а и (5 наречен извита сектор (фиг. 17). За да се определи областта на извития сектор OAVO razobsmsgo в п произволни части лъчи п означават ъглите между лъчите чрез вземат произволно лъч затворено между и означават п.к. дължина на вектора на радиус, съответстващ на лъча. разгледаме кръгов сектор с радиус равен на РК и централен ъгъл Ay> * (фиг. 18). Площта AQk е равна или, както п.к. = фиг. 18 Правейки такава ще изгради IX всички сектор п части ИНФОРМАЦИЯ НА получи фигура, състояща се от п кръгови сектори, площ Qn което е равно на означават най-големият чрез L: пл плоска форма в полярни координати Изчисляване обеми органи дължина крива дължина Изчисляване в правоъгълна координира дължината крива на кривата, определена от в параметрична форма на кривата в полярен дължина координати Ние разделят ъгъл в на AO все по-малки парчета, така че 0. След това, получената фигура ще бъде по-малко и по-малко се отклоняват от сектор OAVO и затова естествено да се предположи, Q площ от границата на извития сектор OAVO Qn изградени личности направите грешка при. при условие, че съществува тази граница и не зависи от това колко сегмента на дял [а, п) в частични сегменти, както и точките за избор, за да ги. По този начин, по дефиниция, ние имаме един Сума 2 е неразделна функция сума, която е непрекъсната върху интервала [а, (5 \ от непрекъснатост на функция / (ш?). Следователно, това количество, когато А G е ограничение равно определен неразделна F 2М DF . по този начин областта на извития сектор е OAVO Пример 1. Виж областта на фигурата, ограничена от кардиоидна областта за търсене се 0,2 2 «§ 12. Изчисляване на обема на органите Помислете тяло ограничена от затворена повърхност. Нека Q известна площ на всеки орган сечение равнина, перпендикулярна на оста ох . Тази област зависи от положението на равнината на рязане, т.е. функция на х (Фигура 20).: .. Предполагаме, че функцията е непрекъсната върху интервала [а, Ь). За да се определи обхвата на провеждане равнина на тялото. който razobyuttelo в п слоеве. При всеки интервал [X, п, поеме една произволна точка К и замени всеки орган слой цилиндър с образуващите, успоредна на оста Ox, указание, което е част от контура на тялото на равнина X = (к (Фигура 20) Обем Avk като цилиндър е .. продукт на областта, където е на основата на нейната височина Akhk :. и обем V на "всички п цилиндъра ще бъде сумата от 0, то е естествено да се =) FC = I Ако това количество е ограничение като = макс да * за обем V на тялото? в този случай, размерът на 2 е от неразделна размер на функция Q (х), непрекъснато на интервала [а, 6], и поета CB определен срок и има определен интеграл на пример 1. Изчислява се обема на тялото, ограничена от елипсоид размер равнина фигура r2 в полярни координати Изчисляване Изчисляване на дължина от дължината крива на кривата в правоъгълна обеми тяло координира дължината на кривата посочено в дължината на параметри формата на кривата в полярни координати в раздел 4 елипсоид от равнина, перпендикулярна на оста х и съответните абсциса получа елипса (фиг. 21) или полу-ос, които са -Therefore площ Q (х) е равна на напречното сечение Прилагането на формула (1), ние получаваме По-специално, когато елипсоида се изтегля в сфера. и обем е равен разгледаме тяло, образувано чрез завъртане около оста Ox AVA извити трапец (фиг. 22), ограничена от крива у = F (х) у Ox и прав. Това тяло се нарича тялото на революция. равнината на въртене на секцията на корпуса, перпендикулярна на оста х и съответстваща на абсцисата X, квадрат е кръг. Следователно, количеството на въртене на тялото 4 уравнението на параболата е дъга ОА. Вие обем е §13. Изчисляване на дължината на кривата пример 2. Виж обема на тялото на въртене, получена чрез завъртане дъга от парабола OA У2 = 2px около оста Ox (fig.23). Fig.23 Помислете крива ^ AB като завършва в точките А и В, а ние го приемаме за произволна точка М \. след по крива, една след друга (фиг. 24). Свържете тези точки .dliny акорди, които са обозначени с. Тогава Sn дължина от прекъснатата линия. вписан в кривата ^ AB, ще бъде равна на Definition. Дължина S ^ AB на кривата е границата, до която има тенденция дължина 5 "на вписан многоъгълник, когато дължината на максималното си ниво до нула: ако съществува тази граница и не зависи от избора на точките на кривата в този случай кривата ^ AB наречен може да се коригира. "Фиг. 24 13.1. Дължината на правоъгълна координира WAV кривата предположим, че кривата определя от уравнението у = F (х) у където е (х) функция има непрекъснат производно / '(х) на [а, Ь]. Разделете интервала [а, произволни точки в N елементарни интервали и ATG конструктът вписан полилинии върховете на които са точки на у крива = / (I): Означаваме Р. добавки за многоъгълни единици чрез PCRs и след това определя дължина FC-ро връзка е многоъгълни (фигура . 25) Използване теорема Лагранж, където - някои точка на сегмента (xjk.ii «JK на). Поради това, дължината на вписан многоъгълника е равна От състоянието на F '(х) е непрекъсната върху [а, 6], функцията е непрекъсната в този интервал, и следователно неразделна сумата (1) има граница на S макс. която се определя от интеграл: или, накратко, от точка от уравнение контактната мрежа намери Имайки идентичност получаване областта на равнина фигура в полярни координати Изчисляване обеми органи изчисляване на дължината на кривата на дължината на кривата в правоъгълна координира дължината на кривата посочено в параметри формата на дължината на кривата в полярни координати Следователно Пример 1 . Изчислява дължина 5 контактната мрежа. Дължината на кривата, дадени в параметрична форма Нека ^ AB крива, дадена в параметрична форма, където функциите и уравненията) имат непрекъснати производни на сегмента. където на този сегмент. В този случай уравнение (3) определя функция у = / (х) с непрекъснато производно на y'x = F]. След това, съгласно формула (2) или пример 2. Изчисли дължината на окръжност с радиус R (фиг. 27). 4 обиколка параметри формата, дадена от уравнения. Според уравнение (4) дава Пример 3. намери дължината на елипсата. След това, като се използва формула (4) и като се вземат предвид симетрията на елипса спрямо координатните оси, където намери "- ексцентрицитета на елипсовидна. Имаме т.нар елипсовидна неразделна *, която не се изчислява чрез директно прилагане на формулата на Нютон-Лайбниц, тъй примитивното не е елементарна функция. + Забележка. Ако сложите. Ооо получаваме, че е в този последен запис ние се интересуваме от интеграла обикновено се смята. Пример 4. Намиране дължина на един -arki "циклоида дължина крива в полярни координати Нека WAV крива даден от уравнение в полярни координати R, където / (у?) Има непрекъсната производно) на сегмента за намиране дължината на крива му параметри уравнение. За тази цел ние използваме формули преход от полярен да декартови координати. Заместването р функция / (в?), Ние получаваме уравнението. които са на параметричните уравнения на кривата. Тук аргумент е ъгъл у полярен. Разнообразяване на последното уравнение, ние откриваме. Squaring двете страни и добавяне на всеки равенство, ние с формула (4), ние получаваме или, еквивалентно, (6) Пример 5. дължина Изчисли кардиоидна кардиоидна намери от Eq. Прилагането на формулата (б), виждаме, че