Пълен линеен коефициент на затихване на лъчението в материята, общност за атомна български
В тази статия ние ще обсъдим въпроса числено максимално отслабване на гама от - радиация вещество в зависимост от енергията на гама - кванти. Зависимостта на минималната обща коефициент на линейно намаляване на гама - лъчи в значение на атомни номера на елементите - кривата на прозрачност. В максимуми на тази крива съдържат благородни метали - никел, родий, осмий с голям коефициент на абсорбция на лъчението в прозрачна област със същия модел на електрони пълнене външните обвивки.
Гама радиация има висока проникваща способност. Гама лъчите взаимодействат с ядрата и електроните на атомите на средата и се отстраняват от сноп от фотоелектричния ефект, Compton - ефект и ефект на електрон - позитрон двойки [1]. Колкото повече ефекти действие, по-малко проникваща способност на гама радиация. При ниски енергии γ-лъчи (до десети MeV), сравними с energiiey йонизация, се наблюдава фотоелектричния ефект. В фотонни енергии Eγ ≥1.02 MeV, има ефекта на електрон-позитрон двойки. Ефект Compton ефект настъпва в междинно съединение енергия регион [1]. Комбинираното действие на въздействието се характеризира с пълна линеен коефициент на отслабване γ лъчи в значение - τ. Оказва се, че зависимостта на коефициента на излъчване на затихване на фотонна енергия е ниско (прозрачност за излъчване) [1] .За изкуство проникваща способност у лъчи е особено голям. Ако се изисква затихване γ лъчи в дадено вещество в обхвата на прозрачност, много повече ще отслаби радиация в останалата част от енергията. В този документ от числения експеримент изследва свойствата на прозрачен участък за всички химически чистите вещества.
Изявление на проблема
Пълен линеен коефициент гама-лъчи затихване се изчислява по формула [1]:
Когато п е концентрацията на абсорбиращи атоми за единица обем, σ -complete ефективен участък затихване. Интензитетът на лъча I (х) се променя от дебелината х последния слой:
I (0) е интензивността на лъча в началото. Концентрацията на N-атома на средата може да бъде изразена от р на средна плътност, броят на Авогадро Na, атоми средно молекулна маса М:
Заместването п с формула (2) в (1):
Общ линеен коефициент на отслабване т се изразява чрез формула [1]:
някъде σf, σk, σpar напречните сечения за фотоелектричния ефект, Комптън - ефект и производство двойка, съответно. σk Z е множител (4) като разсейване центрове за Z фотони са електроните в ефекта Compton, а в останалите ефекти на центровете за разсейване са атома. Формула, предложен от учителите на Министерството на Общото Ядрена физика на Министерството на Московския държавен университет физика, за σf. σk. σpar са [2]:
когато:
-безразмерна параметър гама-лъчи енергия,
- класическа радиус електрон, Z е заряда на ядрото
- фина структура константа, ме * С 2 - енергията на електрон в покой.
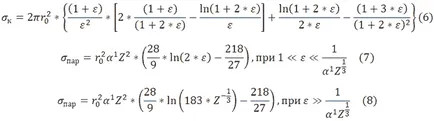
Напречното сечение на електрон - позитрон двойки σpar във формули (7) и (8), изработен в асимптотичната граница на ε »1. Реакционната Сечение σ има смисъл площ обструкция поток от частици на един атом. Има физически смисъл само σ ≥ 0. В формула (7) ≥0 σpar с ε ≥ 6.7 .Although двойки са в енергия на гама лъчи MeV Eγ ≥1.02, или
Това ограничава обхвата на приложимостта на формула (7) .Въпреки тежки ядра прозрачен участък (минимум пълно линеен коефициент на поглъщане гама-лъчи τ (ε)) се постига дори ако ε <6. Итак, задача сводится к поиску точки минимума функции τ (ε ) с использованием уравнений (4)-(8).
Програми написани на Fortran (Compaq Visual Fortran Professional Edition 6.6.0). За конструиране на функция т (ε) числено решаване на системата на алгебрични уравнения (4) и (5) (6), (7) и (8). За да се увеличи програмата за сближаване е писано в двойна точност, т.е.. Д. Integer и реални променливи са точни ЦЯЛО (8), REAL (8), съответно. Всички физически величини -. Плътност, молекулна маса и т.н. са заместени с най-малко пет значими цифри от директорията "физически величини" [3]. Във формулите (7) и (8) за σ ≥ 0 използване смяна
Ако σpar ≥ 0, σpar = σpar. Ако σpar <0, то σпар ' = 0. Таким образом, σпар ' имеет физический смысл для всех значений ε. В ядерной физике в небольшом интервале изменения заряда ядра Z трудно выполнить неравенства ≫ или ≪, к тому же двойные. Знак во много раз больше заменим знаком больше. Окончательно σпар ':
където: σpar (7) σpar (8) - означава σpar изчисление от формули (7) и (8). Въпреки това, за светлина ядра минути (τ (ε)) се постига с εmin = (20-140), (t.e.εmin "едно малко удовлетворени).
Модул за кандидатстване | σpar | Това води до т на фрактурата функция (ε), която е гладка функция на превключвателите в гладка непрекъсната функция по части (Фиг.1). Fracture загладени функция dcscon програма повикване (п, XDATA, fdata, ibreak, почивка, cscoef), използвайки imsl библиотека (използване dfimsl) [4]. В загладени крива се конструира от dcscon. доста плътно следва оригиналната крива запазва посоката на изпъкналост във всички области. N е броя на точките за въвеждане на данни, Xdata, fdata-X, Y координати на точки, изгладеното стойност на функция, са в cscoef масив (1,2 * п), cscoef на измерение (4,2 * п).
Фигури 1 и 2 в зависимост т (ε) чрез използване на формули (4), (5), (6), (9) ", за да води. Фигури 1 и 2 са екстремни стойности
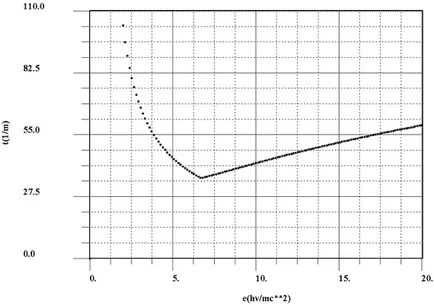
Фиг.1 Зависимост на τ (ε) за олово (без изглаждане).
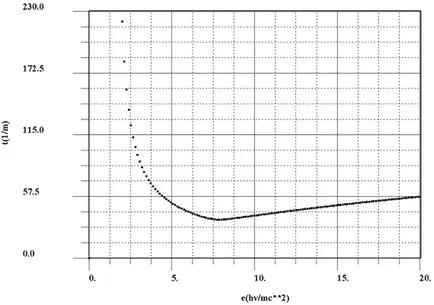
2. Зависимост на τ (ε) за олово (изравняваща).
(Εmin = 6.67, τmin = 35.77 m-1) и (εmin = 7.733, τmin = 35.77 m -1) съответно. Имайте предвид, че стойността τmin = 35,77 m -1 не се промени за една малка промяна εmin след изглаждане на работа. В действителност, на местно екстремум за гладка функция на промяната в неговата стойност е стойността на една малка поръчка. от промяната в спора. Дебелината на полу-затихване намери формулата:
Тези стойности са в добро съгласие с таблични данни за усвояването на гама-лъчи с олово.
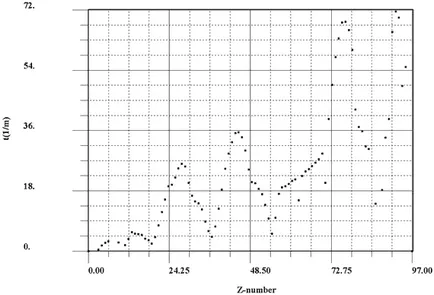
Изграждане prvodilos функции на химически чиста елементи 87, с изключение на газове с ниска температура на втечняване и елементи с неизвестен плътност. Са координатите на крайни точки (εmin. Τmin), за някои елементи Z (Фигура 3). За леки елементи Z ≤ 40 за тези координати съвпада конвенционална и загладени крива. Както бе споменато по-горе, τmin стойност зависи малко на операция на изглаждане за всички Z. Фигура 4 е дадена графика τmin (Z) от стойностите на загладени точки Фиг.3 програма dcscon. Ние наричаме тази крива кривата на прозрачност за гама - кванти.
Кривите на Фигура 3 и Фигура 4 са дълбоко минимуми в пункта, съответстващи на алкални метали: калиев K19 τmin = 2,208 м -1 (. Венче електрони обвивка 4s 1)
рубидий Rb37 τmin = 4,275 м -1 (5 vn.obolochka S 1),
цезиев Cs55τmin = 5,209 m 1 (vn.obolochka 6 S 1). Изключение в тази група се оказа радон. Rn86τmin = 14.15 m -1 (S vn.obolochka 6 1 6 6p) -Като за точност към него алкални Франция имат плътност в таблиците [3] и точка на фиг.4.
Може би за Франция трябва да бъде последният местен минимум на фигура 4
Кривата на фигура 4 има максимуми при пункта, съответстващи преход (благородни метали):
1) максимален никел Ni28τmin = 26.01 m -1 (vn.elektronnaya обвивка 3d 8 4s 2), на следващия елемент
Su29 меден (vn.elektronnaya обвивка 3d 10 4s 1)
2) максимално за родий Rh45 τmin = 35.47 метра -1 (vn.obolochka 5S 4 8 1 г), на следващия елемент паладий Pd46 (Int. 10 4d електрони обвивка 4s 1)
3) максимално за иридий Ir77τmin = 76.6 m -1 (г vn.obolochka 5 7 2 6S), следната елемент платина Pt78 (вътр. 5d електрон черупка 9 6s 1).
Същият модел за запълване на външните електронен слой дава увереност в правилното определяне на елементите в екстремните точки на кривата на фигура 4 за Ni28. Rh45, Ir77.

Фигура 3. минимална стойност на общия линеен затихване КОЕФИЦИЕНТА
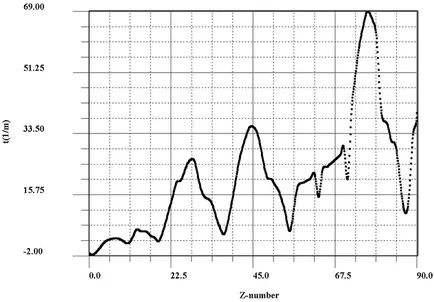
Фигура 4. прозрачност крива на гама лъчи.
Анализ екстремум точка, ние виждаме, че минимуми са оформени в фиг.4 алкални метали с малък йонизационна енергия. Това техните външни електрони взаимодействат с гама лъчи може механизъм Compton ефект. Фиг.3 максимуми заемат благородните метали от група 8 на Менделеев таблица.
Те са пълни с 3d, 4d, 5d електрони обвивка. Всички те се увеличи броят на г-орбитали от по 2 единици с увеличаване на ядрената таксата по един. В същото време, обикновено това се случва umenshnie орбитален и стая единица, когато се увеличава ядрените безвъзмездно от една единица. В този случай, промяна в състава на две черупки. Може би техните електрони имат сходни енергии и вероятности сравнима Vero взаимодействие с гама-лъчи. Такива елементи в таблицата са само три.
Изненадващи Свойства на благородни метали. Те имат малък ефективен атомен радиус. Малки ефективни атомни радиуси са съседни заобикалящата Ni28. Rh45. Ir77 елементи. Електроните на тези елементи имат значително енергия с ядрото. модул на Юнг голям ENI = (200-220) GPa, ERH = 385GPa, EiR = (520-590) GPa (и висок коефициент скованост на пробата). Следователно, трудно е да се деформира на електронен слой от благородни елементи [3]. В Ni28. Rh45. Ir77 подобни електрически и термични свойства
Всички по-горе показва, че благородни метали Ni28 на. Rh45. Ir77 гама - квантите ефективни г електрони взаимодействат черупки черупки и S. При което енергията на електроните на тези пликове са сравними.
резултати:
1) числово проблем зависимост пълна линеен коефициент на поглъщане на енергия гама-лъчи вещество от последната.
2) Задачата взема предвид главно проникваща радиация спектър на излъчване на енергия.
3) зависимостта на пълен коефициент на линейна абсорбция на заряда на ядрата в прозрачността на гама-кванти.
4) Прозрачност минимуми на кривата запълване на алкални метали.
5) крива Прозрачност максимуми съответства благородни метали Ni28. Rh45. Ir77, със същия модел на запълване на външните електронен слой
6) Ni28 метали. Rh45. Ir77 групи образуват центрове Z на подобни елементи с голяма общия линеен коефициент на поглъщане гама кванти. Тези елементи или техни сплави с по-общи елементи могат да бъдат ефективно използвани за усвояване на гама радиация.