Питагоровата номер 1967 Перелман I

питагорейските числа

Удобен и много точен метод, използван за геодезически приземните перпендикулярни линии, е както следва. Нека през точка А се изисква да се подредят MN перпендикулярна (фиг. 13). А лежи в посоката на AM три пъти на ден и разстоянието. След това затегнете кабела три възли, разстоянията между тях са равни на 4а и 5а. Поставянето на крайни възли с точките А и В, дръпне въжето от средната възел. Шнура намира триъгълник, при което ъгъл - живеят.

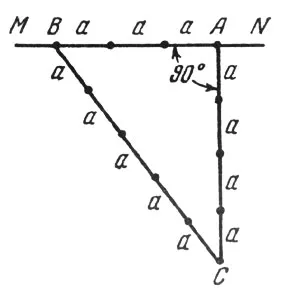
Фиг. 13. Да предположим, че през точка А се изисква да извърши перпендикулярна линия MN

Този древен метод очевидно се отнася дори и преди хилядолетия, строителите на египетските пирамиди, въз основа на факта, че всеки триъгълник, чиито страни са в съотношение 3: 4: 5, в съответствие с най-известните питагорова теорема - правоъгълна, като

Освен номера 3, 4, 5, там са известни безброй положителни числа, а, Ь, с, които отговарят на връзката

Те се наричат питагорейските числа. Според питагорова теорема, тези цифри могат да бъдат дължини на страни на правоъгълен триъгълник; така а и б са посочени като "краката", а с - "хипотенузата".

Ясно е, че ако А, В, С е тройни питагорейските номера, и Ра, Pb, компютър, където Р - цяло число мултипликатор - питагорейските номера. И обратното, ако Питагоровата цифрите имат общ фактор, а след това може да бъде общ фактор те всички нарязани, и отново ще се утрои питагорейските числа. Ето защо, ние първо ще проучи възможностите за трио от сравнително премиер питагорейските числа (останалите са получени от тях чрез умножаване на цяло число фактор п).

Ние показваме, че във всяка от тези тройни и, В, С на един "краката" трябва да бъде дори и другият неравномерно. Нека поговорим "за противното." Ако и двете "крак" А и Б са дори, на четно число е 2 + б 2. средна и "хипотенуза". Това обаче противоречи на факта, че числата A, B, C нямат никакви общи фактори, тъй като трите четни имат общ коефициент 2. По този начин, най-малко един от "краката" а, б е странно.

Остава още една възможност: на "крака" две странни и "хипотенуза" дори. Не е трудно да се докаже, че тя не може да бъде. В действителност, ако "краката" имат формата

След това сумата на техните квадратчета е равно на

т. е. е номер, който когато е разделен от 4 дава остатък 2. Междувременно квадрат всеки четен брой трябва да бъде разделена на четири без остатък. Следователно, сумата от квадратите на две нечетни числа не може да бъде квадрат със четен брой; с други думи, нашите три числа - не Питагоровата.

Така че, от "краката" а, б, един е дори и от друга странно. Следователно, броят на 2 + 2 б е нечетен, следователно, нечетен и "хипотенуза" с.

Предполагаме, за определеност, че е странно "крак", както и дори-б. на равенство

ние лесно се получи:

Мултипликатори C + б и - б, дясната ръка, са сравнително премиер. В действителност, ако тези цифри имат общ основен фактор, различен от единство, а след това този фактор ще бъде разделена и сумата

т. е. 2в номер, 2Ь, и ще имат общ фактор. Тъй като е странно, а след това този фактор е различен от две, и тъй като същите имат общ фактор за броя на, B, C, което, обаче, не може да бъде. Това противоречие показва, че номерата с + б и - б са сравнително премиер.

Но ако продуктът от относително прости числа е точен квадрат, всяка от които е квадрат, т. Е.

Решаването на тази система, ние откриваме:

Така гледани питагорейските числа са на формата

където М и Н - някои сравнително премиер нечетни числа. Читателят може лесно да се провери и да се обърне: за всеки нечетен тип писмено Питагоровата формула даден три числа, а, б, в.

Ето няколко номера на питагоров триъгълник, получени при различен тип:

(Всички други тройни питагорейските номера или имат общ фактор, или съдържат номера по-големи от сто.)

Питагорейските числа имат общо редица интересни функции, които, които посочваме по-долу, без доказателство:

Един от "краката", трябва да се дели на три.
Един от "краката" трябва да е кратно на четири.
Един от Питагоровата номера трябва да бъде кратно на пет.

Читателят може да се провери наличието на тези свойства, гледане на горните примери на групи питагорейските числа.