пасивен две терминал мрежа

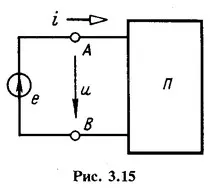
Тока и напрежението на входа на всеки от пасивната два терминала мрежа (фиг. 3.15) са свързани чрез закона на Ом

където Z и Y - вход интегрирани два терминал устойчивост и проводимост.

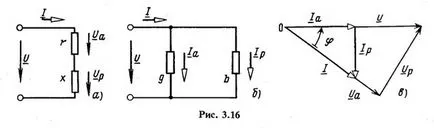
Входен импеданс Z = R + JX отговаря на еквивалентна верига на два терминал мрежа, състояща се от серия свързване на съпротивление и съпротивление R х. Наскоро, според знамението, трябва да се разглежда като един индуктивен или капацитивен като съпротивление. Поради това, в еквивалентна верига (Фиг. 3.16, а) устойчивост х показано условно правоъгълник.
комплекс проводимост

От тези съотношения е видно, че винаги б и х имат един и същ знак.
Например, за веригата на фиг. 3.8 ние получаваме за грам и б са сложни изрази не само б. но г зависи от честотата:

Напротив, за веригата на фиг. 3.12. състояща се от паралелно свързване на елементите, получени чрез проста експресия на проводимостта, но относително сложни изрази за съпротивления и където еквивалентно съпротивление зависи от честотата. Според (3.36)

Преходът на резистентност Z = R + JX проводимост на Y = грам - йб и обратно съответства на веригата за заместване със сериен връзка елементи на схема R и JX еквивалентна схема на паралелно свързване на елементи грама и -jb и назад (фигура 3.16, и б.).
Напрежението U може да се разложи като:

при което - компонент съвпада във фаза с ток, наречен активен компонент на напрежение; - компонент изместен във фаза по отношение на текущата ъгъл р / 2 се нарича реактивен компонент напрежение.
Компонентите могат да се разглеждат като напрежение на елементите R и S еквивалентна схема.
Фиг. 3.16, е представен във вектор диаграма на две терминал мрежа с J> 0, т.е., ако х - .. на индуктивен реактивно съпротивление. Триъгълник, образуван от векторите с страни пропорционално Z, R, и | х |. Той нарича делта стрес. Такава му триъгълник, чиито страни в произволен мащаб равни съпротивления Z, R, и | х |. Тя се нарича съпротивление триъгълник. От стреса на триъгълник следва, че

Входно комплекс проводимост Y = грам - йб отговаря на еквивалентна верига на два терминал мрежа, състояща се от паралелно свързване на проводимости грама и -jb. Последното, в зависимост от знака на индуктивни или капацитивни. Поради това, в еквивалентна верига (Фиг. 3.16,6) проводимост б. илюстрирано на фантомен правоъгълник. Текущ на входа двуполюсен могат да се разделят на компоненти:

при което - компонент съвпада във фаза с напрежението се нарича активен компонент на тока; - компонент изместен във фаза спрямо напрежението на р / 2, ъгълът се нарича реактивен ток компонент.
Компонентите могат да се считат като течения в елементи G и -jb еквивалентна схема.
Триъгълник, образуван от векторите с страни пропорционална база. гр. | Б |. Той нарича делта течения. Подобно на него триъгълник, чиито страни са в произволен мащаб равни проводимост у един. г и | б |. Тя се нарича триъгълник проводимост.
Сред настоящите триъгълника имат

Пример 3.6.
Схемата се състои от кондензатор с капацитет С = 10 microfarads и резистор с R съпротивление - 100 ома паралелно. За да се определи какво трябва да бъде капацитет на кондензатор и резистор, че когато се обърна серия верига връзка с честота еквивалентна на дадена рад / сек.

Решение.
Проводимост на веригата

Устойчивост на веригата
Еквивалентна схема трябва да има същия съпротива. По този начин, желаното съпротивление на съпротивление от 50 ома. и капацитет С = - 1 / w х = 20 UF.

Пример 3.7.
Напрежението и тока на входа на пасивната две терминал мрежа (вж. Фиг. 3.15)

Определяне параметрите на двете еквивалентни схеми на двуполюсен, активни и реактивни компоненти на напрежение и ток.