Основните правила на диференциация и производни на елементарни функции

Общото правило на диференциация. Когато разграничаване функция (намиране на неговите производни) се придържат към следната схема:

избиране на стойност на х. дай му priraschenieh и да намерят стойност в функция tochkeh + h. ravnoef (х + x);

до отношението f / x и, ако е възможно, да го опрости;

намери производната на функцията, която е на границата

(f / x). ако съществува тази граница:

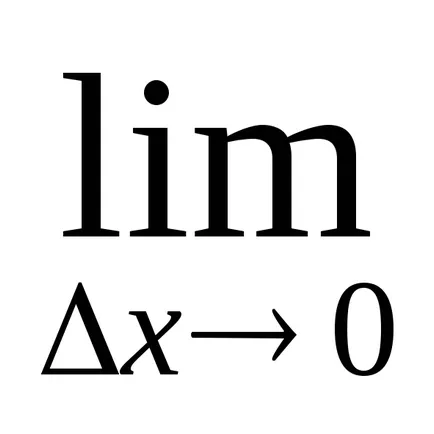
Производното на алгебрични сумата от диференцируеми функции е равна на сумата от алгебрични производните на тези функции.

Производно продукт на две диференцируеми функции е равна на сумата на продуктите на втората функция на първото производно на първата функция и производното на второто:

Частен производно (фракция) на две функции е фракция, чието знаменател е равна на квадрата на диференцируема функция знаменател и числителя е разликата между продуктите и производното на знаменател и числителя на числителя на знаменател на производното:

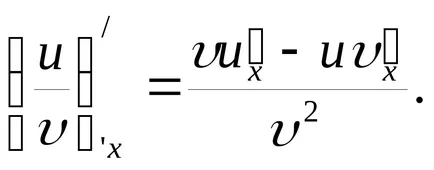
ПРОИЗВОДНИ сложни функции.

Всеки комплекс функция може да бъде представен под формата на елементарни функции, които са негови междинни аргументи.