Определяне на инерционен момент на физическо махало

Фамилия и инициали Група _____________ ______ ______ Дата

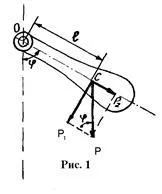
Физическото тяло махало наречен укрепен при фиксирана хоризонтална ос не преминава през центъра на тежестта, както и в състояние да се люлее около тази ос (фиг. 1)

Gravity физически махало Р може да се счита, прикрепен към центъра на тежестта на махалото S. отклонява под малък ъгъл # 966; от равновесното положение, ще

Определяне на инерционен момент на физическо махало

премести под въздействието на гравитацията сила компонент Р1. че при малки ъгли на отклонение е приблизително равна на:

знак минус означава, че операционната сила е насочена надолу ъгъл # 966; ,

В момента на тази сила по отношение на оста на въртене е равна на

Под влияние на тази точка, тялото придобива ъглово ускорение. равно. където I - инерционен момент на оста на въртене.

Заместването на този израз, вместо на стойността на М (1) и. Ние се получи.

Сравнявайки този израз с уравнението на хармонични трептения. можете да пишете. но. означава. когато:

Редът на изпълнение

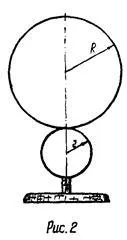
1. Като физически махало, моментът на инерция се определя, двете са свързани заедно с метален диск (фиг. 2). Двете дискове могат да се колебаят около ос, преминаваща през центъра на голямо диск. Използване mm линийка за измерване на диаметъра и дебелината на големи и малки дискове, и познаването на плътността на материали дискове (7,8 · 10³ кг / m³) за изчисляване на теглото на всеки диск от формулата:

където G = 9,81 m / s².

2. Центърът на тежестта на двата диска се определя от следните съображения: празен диск центрове са разположени на една и съща хоризонтална линия. Към центъра на тежестта на всеки диск, разположен в центровете на дисковете се прилагат мощност Р1 и Р2 на тежестта. Радиусите на диск R и R.

Центъра на тежестта на системата, състояща се от два диска, се намира в точка С, който е на разстояние # 8467; точка Р2 на прилагане на силата и на разстояние R = R - # 8467; от точката на прилагане на сила Р1. От закона за равенство на моменти на оръжие за центъра на тежестта на системата P2 # 8729; # 8467; Р1 = (R + R - # 8467) се определя от разстоянието # 8467; от оста на въртене до центъра на тежестта

3. Отхвърляне на махалото под лек ъгъл, я освободите и го оставете да се люлее свободно. Измерва се времето т 20 пълни трептения и за определяне на трептене период Т.

където п - броят на пълните трептения.

4. Познаването на периода на махалото и теглото Р = Р1 + Р2. определи момента на инерция на махалото по формулата:

5. Всички данни се записват в таблицата

1. Какво се нарича колебания?

2. Какво се наричат хармонични трептения?

3. Какво се казва, амплитуда, фаза, началната фаза, за период от цикличен честота на трептене?

4.Risunok хармонични трептения. Цифрата показва амплитудата, период, начална фаза.

5. Какво се нарича физическо и математическо махало?

6Zapishite уравнение физически трептения махало.

колебания 7. Какъв се наричат свободни?

8. Как се наричат квази-еластична сила? От това, което принуждава вибрациите на тялото да се появят в работата?

9.Pri всяко физическо колебае махало може да се счита хармоничен?

10. Какво се нарича намалената дължина на физическото махало?

11. Как да променя честотата на природните колебания на прост махало вибриращо с увеличаване на телесното тегло два пъти? с увеличаване на продължителността на два пъти? Същото за физическото махалото.

12. Как да променя кинетичната, потенциал и общата енергия на един прост махало във времето?