Определяне на график всички стойности на момента на силата на триене и да намерят своята средна стойност
2. Определяне на график всички стойности на момента на силата на триене и да я намерите средно. Сравнете този резултат с предварително измерената в работата.
Целева 3. Сравнение на измерените и изчислените стойности на моментите на инерцията
1. Напишете в Таблица 2.4 доклади на измерените стойности на инерционни моменти на махалото.
2. С помощта на формулата за изчисляване на инерционни моменти геометрично редовни органи и теорема на Хюйгенс - Щайнер изчисляване инерционни моменти на макари, кръстове и други стоки, въртящи се около оста не преминава през тяхната средна. Данните за изчисляване са взети от "паспорт" на устройството. Общият инерционният момент на махалото се определя чрез сумиране на инерционни моменти на частите на махалото.
3. Сравнение на изчислените и измерените стойности на инерционните моменти. Намери относителните отклонения между изчислените и измерените инерционни моменти.
ОПРЕДЕЛЯНЕ инерционен момент И ПРОВЕРКА НА теорема Хюйгенс-Щайнер
ОТ вибрации при усукване
Целта на експериментална проверка на теоремата на Хюйгенс - Щайнер и решаващи моменти на инерция на телата на проста форма. Идеята на експеримента
Експериментът използва връзката между периода на трептене на торсионна махало и инерционен момент. Както махало избран кръгла платформа, суспендиран в гравитационното поле на три дълги нишки (trifilyarny суспензия). Платформата може да изпълнява усукване колебания около вертикална ос. На тялото платформа на различни форми поставен, измерена периоди на трептене на махалото и се определя стойности на моментите на инерцията на телата. Теорема Хюйгенс - Щайнер проверени за съответствие между експериментални и теоретични зависимости инерционни моменти натоварвания върху тяхното разстояние до центъра на платформата на.

където w - ъглова скорост на въртене, J - инерционен момент спрямо оста на въртене М - момент на външни сили спрямо тази ос.
Теорема на Хюйгенс - Щайнер. Ако инерционният момент по отношение на оста на въртене, преминаващи през центъра на масата е на стойност J0. че по отношение на всяка друга ос на разстояние една от първата и е успоредна на нея, тя ще бъде равна на
където m - масата на тялото.
За да се уверите теоремата Хюйгенс - Щайнер учи в тази работа на вибрациите при усукване на тялото trifilyarnom окачване твърдо. Trifilyarny платформа суспензия е кръгъл радиус R, окачен на три симетрично разположени нишки еднаква дължина подсилени в краищата от тях (виж фиг. 8). Над тези прежди са симетрично прикрепен към диска на по-малък размер (радиус R). Платформата може да изпълнява усукване колебания около вертикалната ос, OO ¢, перпендикулярно на неговата равнина и минаваща през центъра му. Подобна платформа движение води до промяна в положението на центъра на тежестта на височината.
Ако платформата на маса m, въртяща се в една посока, нарасна до височина часа, след което
нарастването на потенциалната му енергия е равна на
където г - земното ускорение. Завъртането в другата посока, платформата въпрос за равновесно положение (H = 0) с кинетична енергия, равна на
където J - инерционен момент на платформата, W0 - ъгловата скорост на въртене на платформата в момента преминава равновесното положение.
Пренебрегването на работата на силите на триене, на базата на закона за запазване на механичната енергия, ние имаме:
Ако приемем, че платформата извършва хармонични вибрациите при усукване може да бъдат записани от времевата зависимост на ъгловото преместване на платформа под формата на т
където - ъглово отместване на платформа, A0 - максималния ъгъл на въртене на платформата, т.е. амплитудата на ъгловото преместване, Т - колебание период. За ъгловата скорост w, който е първи път производно на величината на изместване могат да бъдат написани
В моменти на преминаване на платформата чрез равновесното положение (т = 0, 0.5T, ...), количеството w (т) е максимална и е равна на
От изразите (3.5) и (3.8) следва, че
Ако дължината L на суспензия с нажежаема жичка, R - разстоянието от центъра на платформата на нишките на фиксиращите точки по нея, г - радиусът на горния диск (. Фигура 8), е лесно да се види, че
и с максимално отклонение от платформата от равновесното положение
В малки ъгли на отклонение a0 синуса на ъгъла може да се замени с стойност a0. Като се има предвид също така, че когато R< Законът за запазване на енергията (2.9) приема формата: което означава, че Според формула (3.16) може да бъде експериментално определяне на инерционният момент на празен платформа или платформа тяло положи върху него, тъй като всички количества от дясната страна на формулата е пряко измерени. Трябва да се помни, че м - е общата маса на тестовата платформа и тялото лежи върху него. Вид на инсталация е показано на Фигура 8. Съотношението на радиуса на дължината на суспензия платформа са прежди R / л <0,05, что соответствует приближениям, используемым при выводе формулы (3.16). Телата на платформата трябва да бъдат поставени строго симетрични, така че да не е изкривено платформа. За да се улесни определянето на позицията на стоки и по-точно да ги инсталирате на платформата изобразени радиални линии и концентрични кръгове на известно разстояние един от друг (5 mm). Въртене импулс изисква да предизвика усукващите трептения, съгласно платформа от горния диск въртящ се около оста си. Това се постига с помощта на лост, монтиран върху горния диск. Когато такава възбуда почти никой друг трептене, чието присъствие усложнява измерването. В измерванията, използвайте неприемливи вибрационни амплитуди по-големи от 10 °. Измерване на трептенията може да се извърши ръчно или с помощта на хронометър или таймер. Целева 1. Измерване на инерционния момент на празен платформа Измерване и обработка на резултатите 1. инерционният момент на празната платформа JPL определя от (3.16). Така периодът на колебание T платформа изпразване му грешка определи експериментално, и стойностите на L, R, R, m и техните грешки са в постоянен монтаж. 2. Съобщава платформа ротационен импулс и броя на tnekotorogo време (N = 15 -20) пълни трептения. Такова измерване се повтаря 3 - 5 пъти. Получените резултати са въведени в таблица 3.1 от доклада. 3. Съгласно експерименталните данни за всеки експеримент са стойността на периода на усукване колебание. 4. Намерете средната стойност и общата грешка на периода на трептене. В тази систематична грешка в периода на оценяване, може да се приема като равни. 5. Изчислете инерционният момент JplE платформа. Намерете стойността на относителната и абсолютната грешка за инерционният момент на платформата. 6. Изчислете теоретична инерционен момент JplT платформа. въз основа на своето тегло и размер. Намери грешки от това изчисление. 7. Сравнение измерва експериментално и теоретично изчислена стойност на инерционния момент на празен платформата. Посочете какъв процент от експерименталната стойност се различава от теоретичната :. Задача 2. Определяне на инерционните моменти тела с предварително определена форма Измерване и обработка на резултатите 1. Платформа последователно зареден проучени органи, така че техният център на тежестта съвпада с оста на въртене на платформата. Както органи тест плоча са избрани с формата на квадрат, правоъгълник, равностранен триъгълник, диск, както и други форми на правилна геометрична тяло. 2. Измерете брой трептения по време на цялата система. За всяко измерване тяло се извършва 3 - 5 пъти. Резултатите от измерването са вписани в Таблица 3.2 на доклада. 3. Изчислете моментите на инерцията JN на натоварените платформи и техните грешки. Трябва да се отбележи, че в уравнение (3.16) трябва да се заменя със сумата от масата на тялото и платформа като в грешка грешка грешка формула тегло равно на общото телесно тегло и платформата. 4. Използване на факта, че в момента на инерция - добавка количество се изчислява моменти на инерционни органи: JE = JN - JplE. Намери абсолютната стойност и относителна грешка за инерционни моменти органи. 5. Сравнение на експериментално получените стойности на инерционни моменти с изчисленото теоретично (вж. Приложението 3). Изчислените резултати се въвеждат в таблица 3.3 от доклада. Задача 3. Проверете теорема на Хюйгенс - Щайнер Теорема 1. За да проверите Хюйгенс - Щайнер се използват два или няколко подобни организации, които имат цилиндрична форма. 2. Инсталиране на товари в центъра на платформата, те се поставят на една от друга. Вълнение усукване вибрации платформа. Измерва се времето Т няколко трептения (N = 15 - 20). Данните се въвеждат в таблица 3.4 от доклада. 3. включва симетрични товари на платформата по отношение на оста на въртене. Извършва време вибрации измерване в продължение на 5 - 7 позиции на стоки, постепенно ги движи към краищата на платформата. 3.4 таблични стойности на разстоянието от центъра на масата на всеки орган и центъра на платформата, а броят на трептения N TN време тези вибрации. Обработка на резултатите 1. 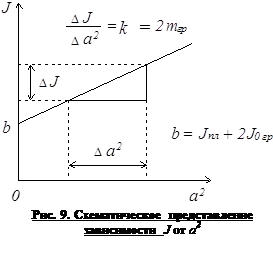
2. таблични стойности на две.
3. За всяка позиция са карго инерционен момент Джи с платформа товари от формула (3.16).
4. Получените стойности на момента на инерция Ji се прилагат към графиката на инерционният момент на органи системата на квадратен разстоянието до центъра на масата на стоки и оста на въртене 2 (схематично тази връзка е показан на фиг. 9). Както следва от теоремата на Хюйгенс - Steiner, тази графика трябва да бъде права линия с ъглов коефициент
са- числено равни 2mgr. където мгр - масата на товара. Също така, пресечната ординатната ос е сумата от моментите на инерцията на разтоварените товари на платформата и инерционни моменти JPL + б = 2J0gr.
5. От зависимост J = F (2) определяне на стойността и на стойност мгр б. Сравнявайки получената стойност с товара, който се използва в работата, и получената стойност б с изчислената стойност. Съвпадението на тези стойности (за грешки изчисления) също потвърждава, теорема на Хюйгенс-Щайнер.
ОПРЕДЕЛЯНЕ инерционен момент ръкохватката на силите на триене в лагерите Цел
КОЛЕЛА и моментите на силите на триене в лагерите
Определяне на инерционния момент на колелото и в момента на силата на триене в лагера, като се използва закона за запазване и преобразуване на енергия. Идеята на експеримента
Експериментът използва масивна колело, монтирано върху хоризонтална шахта. Колелото се задвижва от рана кабел върху вала, който е прикрепен към края на товара.
Момент на инерция - мярка на тялото инерция на въртеливото движение. Трябва да се има предвид, че, като цяло, инерционният момент може да има различни стойности по отношение на различните оси на въртене на тялото. Ако тялото е произволна форма и произволно разпределение на масата, инерционен момент може да се определи чрез сумиране само приблизителна
,
където ри - разстояние от оста на въртене на I-елементарния маса DMI.
Ако тялото е с правилна геометрична форма и с постоянна плътност в целия обем, сумата може да бъде заменен от интеграция за целия обем

За изчисляване на инерционни моменти тела с проста геометрична форма (диск, прът, квадрат, и т.н.) обикновено се получават чрез (допълнение 3).
В случаите, когато изчисляването на инерционни моменти на тялото е трудно, да се използва по различни начини, за да ги измерват. Няколко такива методи, дискутирани в този цех. В тази статия ние предлагаме енергия подход за определяне на инерционния момент.
На маховика (фиг. 10) се състои от маховик А неподвижно монтирани върху хоризонталната ос на вала В. В кабел се навива, на края на който е свързан с тегло m, която под силата на тежестта на вала може да бъде сук. При въртене на орган, имащ моменти на сили, които пречат на неговото въртене. Тези точки са главно на силите на триене в опорите и отчасти на силата на съпротивление на въздуха. Последно в тази книга не се счита поради своята незначителност. Големината на момента принуждава Mtr триенето в лагерите може да се настрои, например, състоянието на равновесие М - Mtr = 0, както и загуба на енергия на въртящо се тяло, както се прави в този документ. Спад на потенциална енергия h1 товари mgh1 е насочена към увеличаване на кинетичната енергия на постъпателно
движението на товарни МПС 2/2, за увеличаване на кинетичната енергия JW 2/2 въртеливо движение на маховика и на вала на инструмент и вкарвайки операция Mtr = А й за преодоляване на триенето в лагерите. Според закона за запазване на енергията
където J1 - ъгловото изместване на вала в лагера, съответният обем h1 товара.
Заредете равномерно ускорено движение, без начална скорост, така че
където Т - време понижаване височина h1. Ъгловата скорост на маховика
където R - радиусът на вал Б. момент Mtr триене сила се определя, както следва. Колелото се върти по инерция, вдигнете товар на височина h2 Изразяване на ъгловото път (J1 + J2) през линия (Н1 + Н2) и радиус R на вал, получаваме Този израз е работа формула за измерване Mtr. Заместването в (4.1) стойностите на V, W, Mtr (4.2), (4.3), (4.6), ние получаваме операционната формула за определяне на момента на инерция на маховика При подготовката за измерване на маховик кабел се навива на своя вал да се върти. До края на кабел прикрепен платформата на известно тегло, което товари се прилагат от снимачната площадка да бъдат инсталирани. За да се измери височината на капка корабоплаването h1 и h2 на повишаване на височината на неговото инсталиране в близост до бара на укрепената мащаб. Капка времето за превоз, се измерва с ръчен или фиксирана електронен хронометър. 1. Целева измерване на въртящия момент инерционен момент на маховика и силата на триене 1. шублер се измерва радиус вал. 2. височината на падането на пратката h1 във всички тестове, които могат да вземат едни и същи. Поради това може да бъде предварително измерена като разстоянието между горната предварително избрана позиция на Грузия и позицията си, когато напълно развит мозък. 3. Drum кабел към вала, вдигането на натоварване до избраната точка. Платформата сложи една маса от набор. Мярка време, спад до пълно натоварване амортизира мозък. 4. Измерете височината h2. който се издига товар след развиване на кабела. 5. Опитът с един товар се повтаря най-малко три пъти. След това, се извършват измервания с две и три натоварвания. Всички данни се въвеждат в таблица 4.1 от доклада. 1. От формули (4.6) и (4.7) за всяка точка маса се изчислява сила на триене в лагерите и маховик инерционен момент, чрез заместване на средните стойности на тон и височина h2 от време. 2. Намерете средна стойност от инерционния момент на маховика. Няма никакъв смисъл да се намери средната стойност на момента на силите на триене, тъй като различни натоварвания на вала трябва да имат различни стойности. 3. Грешки при измерване на инерционния момент се предлага да се направи оценка на опита на един от натоварванията. Получената стойност на относителната грешка на инерционен момент може да се прилага към средната стойност на момента на инерция. Стойностите на систематични грешки при измерването на височини h1 и h2 трябва да се вземат на базата на действителните условия на измерване. Грешки на платформата измерване товари равни маси и ± 0.5 гр. Информация за "Кинематика и динамика на движение напред" Категория: Физика
Брой знаци с интервалите: до 136 506
Брой на таблици: 5
Брой снимки: 32