Определяне на ефективния лихвен процент
Ефективен лихвен процент - това е сложна лихва, изчислена на предположението, че всички плащания, необходими за получаването на този заем, ходят на изкуплението си.
Това означава, че ако резултатът от размера на кредита кредитополучателят трябва да направи S0 platezhiR0, R1, R2. RN в точки vremenit0 = 0, t1, t2. TN съответно (което включва и двете плащания на самата заема и от страна на комисията, осигурителни вноски и т.н.), на ефективната лихва е връзка stavkai
Ефективният лихвен процент се използва предимно за сравнение на различните банкови оферти и изчисляването на точната дата на плащанията на Комисията са обикновено неизвестни. Ето защо, ако плащанията се извършват чрез формално редовни интервали, продължителността T (месечни, тримесечни и т.н.), формулата (18.1) има следния вид:
Ако кредитополучателят всички плащания, с изключение може би на първия, същата (R1 = R2 = = Rn = R.), След това в съответствие с формула (17.4) за определяне на съотношението на ефективната лихва ще бъде:
За съжаление, намирането на точната стойност на ефективния лихвен процент, дори и в този сравнително прост случай е невъзможно, така че трябва да го изберете (най-добрия начин - с помощта на специален числен метод). Как точно - това ще бъде обсъдено в следващите параграфи.
Например заема със следните условия:
срока на кредита - 3 години;
лихвен процент (ще означаваме своята й) - 18% годишно;
погасяване схема - месечна равна (фиксирана) с такси;
за таксата за подреждане на кредита - 1% от сумата;
месечна такса за поддържане на сметката на кредита - 0.1% от размера на кредита
Ефективният лихвен процент ще бъде 22,8%. За да се тества се намери стойността на всички променливи присъстват във формула (18.3):
Замествайки тези стойности в (18.3), след намаляване на S0 лесно да се провери валидността на половете (освен ако, разбира се, не обърна внимание на грешката от закръгляване):
Проверете верността на изчисленията на ефективния лихвен процент, можете да използвате нашия калкулатор заем.
Пример заем в размер на 24 хиляди евро, издадени от две години при 12% годишно, платим на месечни вноски в съответствие с диференцирана схема. Аранжиране такси в размер на 1% от сумата. В допълнение, всеки месец на кредитополучателя ще се начислява такса за поддържане на сметката за заем в размер на 0.1% от размера на кредита. Трябва да намерим ефективен лихвен процент на кредита.
На първо място, ние конструираме графика за погасяване на кредита (без плащане структура). В § 11, ние знаем, че плащанията за сметка на погасяване на кредита образуват аритметична прогресия с първоначален срок
А1 = 124 + 0,12⋅112⋅24 000 = 1240 евро
-0,12⋅112⋅24 000⋅124 = -10 евро.
В допълнение, когато се кандидатства за кредитополучателя заем трябваше да плати 0,01 · 24 000 = 240 евро, както и всеки месец с него такса в размер на 0,001 · 24 000 = 24 евро. Следователно, за графика на плащанията по заема е, както следва:
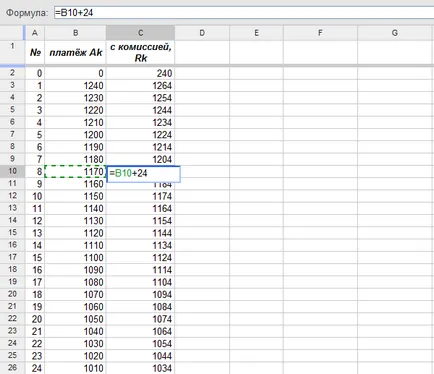
Стойностите на колона "с комисията, Rk". с изключение на първия (индекс 0) съвпада с коефициентите на функцията F в stepenyahx (X), които ще се използват в изчисленията. За първи коефициент (нула stepenix), необходими от първоначалната platezhaR0 = 240 размера на кредита изваждащ (формула горе вляво):
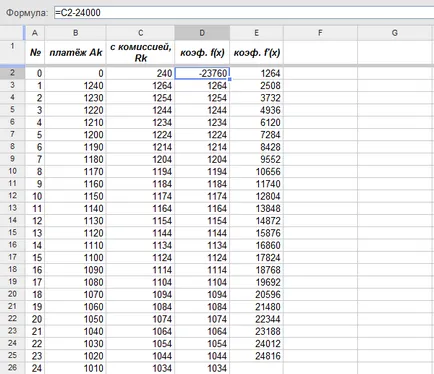
Напомни, ако някой е забравил, че коефициентът брой к на производно коефициент е равен на 1 в nomeromk функция е (х), умножена NAK 1.
Сега, най-накрая, можете да използвате метода на Нютон за намиране на месечна дисконтов фактор (формулата в горния ляв ъгъл):
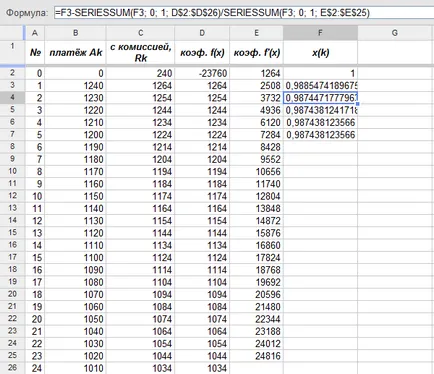
Едновременно с изчисляването на месечната фактор отстъпка се самоопредели ефективен лихвен процент аз:
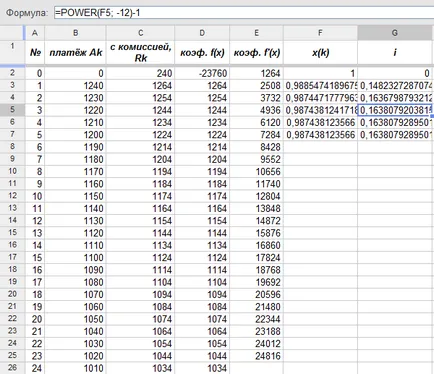
Както в примера в предходния параграф, метод на Нютон ни донесе окончателен отговор само на пет изчисления: на ефективния лихвен процент по кредита се разглежда, е приблизително равно на 16,38%, 4,38% по-висока от номиналната ставка.