Операции на матрици - studopediya

операция имоти матрица допълнение

За всяка матрици А, В и С са със същия размер следните равенства:

1. А + В = B + A (commutativity);

2. (А + В) + C = A + (В + С) = A + B + C (асоциативност).

Продуктът от матрица А = (Aij) номер L е матрица B = (BIJ) на същия размер като матрица А. където BIJ = л Aij. "Аз, к.

Свойствата на размножаването на матрица на броя на

2. L (А + В) = ЗА + LiN (разпределителни над допълнение матрица).

3. (L + M) A = ЗА + mA (разпределителни над присъединителни номера).

Продуктът AB на А и В (m'n размери и n'r съответно) е размера на матрицата С m'r. така че Сий = ai1b1j + a12b2j + ... + AIK bkj + ... + Ен BNJ =

.

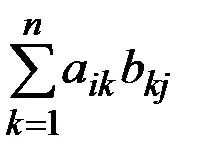
По този начин, всеки елемент Сий. намира в I-ти ред и к тата колона на матрицата С е сума от продуктите на съответните елементи на -тата ред тата колона на матрицата А и й на V. матрицата

Получаване Сий елемент е изобразен схематично така

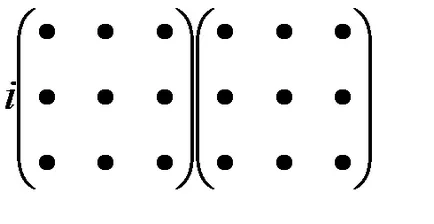
Каталог на AB съществува само ако броят на колоните на матрицата е равен на броя на редовете на матрицата.

Свойствата на операцията умножение матрица

1. (AB) C = A (BC) = ABC (асоциативност).

2. (А + В) C + BC = AC (Distributivity).

3. (В + С) = AB + AC (Distributivity).

4. AV¹VA (офлайн commutativity).

Превключване (или пермутация) са матрици А и В, за които AB = BA.

Матрица, получена от този чрез заместване на всеки от своите линии със същия брой колона, наречена матрица, транспозицията на (А означен T).

1.3.1. Виж линейни комбинации на предварително определени матрици:

1.3.2. Намери продукт на матрици AB и BA (ако има такива):

а)

; б) = (4 0 -2 3 1), ;

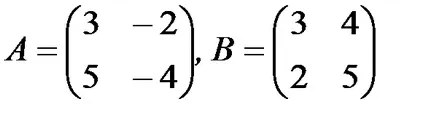
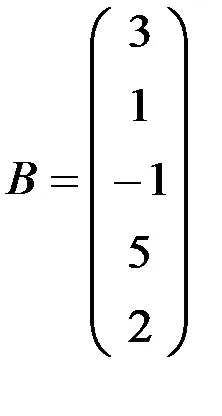
1.3.3. Проверете дали матриците пътуват:

1.3.4. Намери матрица продукт А и АА T T А:

а)

б) = (1, 2, 3, 4); в) .

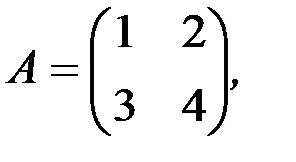
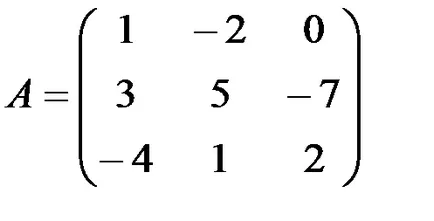
1.3.5. За линейни комбинации от матрици:

1.3.6. Намери произведения на AB и BA (ако е възможно):

1.3.7. Намери произведения на АА Т и Т А: