Обучение за решаване на проблемите в преливането, kvedorelis Наталия Boleslavovna

Този вид проблем се появява по време на Олимпиадата, а понякога - в изпитите.
Като се има предвид няколко кораби с различен капацитет. Попълнете съдове може да се включи. Излишната вода се излива в мивката. Е необходимо, се налива вода в плавателния съд от съда за измерване на предварително определено количество вода, която не съответства на съдовете за сила на звука.
Решете някои проблеми при използването на симулатора ...
Как да се реши проблема с преливане.
2 са дадени капацитета кана 8 и 5 литра. Има чешмяна вода и за източване на вода за миене. Както и при тези две стомна за измерване точно 6 литра вода?

Проблемът може да се формализира в следната таблица:
Математически билярд

Според този метод (което го прави лесен за решаване на проблеми от този тип) трябва да изготви траекторията на топки за билярд, отразена от двете страни на масата, която има формата на успоредник.
Помислете за решаването на предходната проблема.
Страните на успоредник трябва да са с дължина 5 и 8 единици.
От една страна, ние парцел количеството вода в литри на 8-литров кана, и от друга - на 5-литров буркан (виж фиг.).
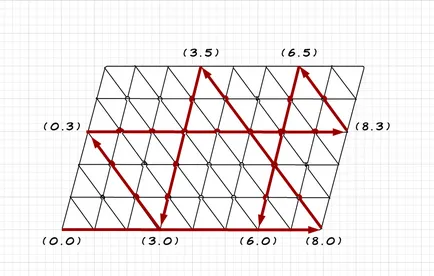
Билярдна топка може да се мести само по линиите, съставящи успоредник решетка. След удря по стените на успоредник, топката се отразява от точката на сблъсък и продължава да се движи по права линия, която преминава от тази точка. В този случай, самата точка описва колко вода е във всеки един от стомните.
Първо, топката е в точката (0,0) и не делви. След това тя се движи по протежение на долната основа на успоредник, докато достигне до дясната страна на точката (8,0). Това означава, че каната 8-литър се напълва с вода напълно и 5-литров - празна.
След размисъл, топката се движи нагоре и наляво, и се удря в горната част на борда (горната страна успоредник) в точката (3,5). Това означава, че в каната 8-литров има само три литра вода и 5 литра се излива в кана на 5 литра.
Проследяване маршрут балон допълнително и записване на всички етапи на неговото движение, докато топката не стигна до точката (6,0) от долната страна, ние се намери решение на този проблем.
три плавателни съдове
Да разгледаме проблема за трите кораба, сумата от съдържанието на който е постоянна.
Контейнерът може да напълни с 9 литра мляко, кутии от 8 литра и 5 литра празна. Задължително да се получи 6 литра мляко. Ясно е, че методът на математически билярд, ние не можем да влязат в точките на успоредник, които определят набор от възможни състояния на системата, в която сумата на координатите надвишава 9.
Решението на този проблем по метода на математически билярд включва използването на така наречените Trilinear координати.
Да разгледаме ABC равностранен триъгълник със страна на и височина Н = А * корен (3/2)
В този случай, триъгълник страна а = 9 * 2 / корена (3) и vysotoyh = 9. Линии, успоредни на страните на триъгълника, ние ще я разделят на равностранен триъгълник с единица височина.
Търсене в този сайт
калкулатор
Превод от един номер система към друга
Converter работи с не-отрицателни числа не по-дълги от 50 символа в двоично число системи за tridtsatishestirichnoy.