Обобщение на дисциплината Математика "десетични дроби

Интересен проблем с десетични дроби ........................ 15

От древни времена за решаване на жизненоважни въпроси хората трябваше да разчита на обектите и да се измери степента, а именно да се отговори на въпроса "Колко?". като овца в стадото, като мерки за зърно, събрани от областта, много мили от селото до областния център и т.н. така има редица. Понякога шеговито казват, математика, "Бог създаде естествени числа, а останалите -. Дело на човека"

Въпреки това, за да се отговори на въпроса "Колко много" естествени числа често не е достатъчен. По този начин, убийството на мамут и да го разделя по равно, на 10 ловци, които не може да се каже "колко мамути" получи всеки. И за дълго време, след като мамутите изчезнали, разделен поравно на три торти на пет от децата си, майка им не може да се каже колко питки, получени всеки. Човечеството е необходимо, за да излезе с нови - фракции - номера, това е, за да излезе с една малка част.

За да отговорим на най-трудните въпроси - като например колко овце в две стада, една от двете фермери събират повече - необходимо, за да се научите как да добавите номера, да ги сравни с друг. Така че, постепенно в продължение на хиляди години, формирана на концепцията за брой. Така че, хората са се научили да се обадя и да напишете номера да прекарат с тях се изчисли и да установи формирането на математически култура, която по-късно е наречен аритметика.

Значителна част от тази вековна начин, ние вече бил в началното училище - точно както за първите 9 месеца на всеки един от нас на ембриона да се превърне в човек, като надвиете на начина, по който го взе на природата милиони години. Сега ние трябва да "оцелее" няколко века на развитието на математиката и първо да прегледат аритметични дробни числа - да се научи да сравнявате фракции с друг, за да ги направи аритметика, и най-важното - да използва тези номера за решаване на практически проблеми.

В 5-ти клас по математика клас, се срещнахме с новата номерация - с фракции. Стана интересно да се знае: "Къде е направил тези числа", "Защо фракции, записани по този начин", "Кой дойде с техните записи", "Да-нататъшното им развитие"?.

За да намерите отговорите на всички тези въпроси, ние се обърнахме към книгите, и в по-модерен помощник на име "Интернет".

Те открили, много интересен материал, с най-интересното, по наше мнение, данните които искате да споделите. Следователно, целта на нашата работа е следната:

Помислете за историята на възникването на фракции. Можете да видите името на първия математик, който даде определението "десетична".

За да се формира умения за извършване на изчисления с десетични дроби, необходими за прилагане на практика;

Вземете интересни и забавни задачи с десетични дроби.

Нови рекордни стойности

Има много различни начини да пишат естествени числа, но в крайна сметка "спечелени" един - десетична позиционна система за записване, който в момента е най-широко разпространени.

Подобна история се случи с фракции рекорд. Фракции се знае, че са възникнали във връзка с разделянето на предмета на няколко равни части.

По този начин, броят на десетичната нотация показва как си число част, и за числител и знаменател на дробна част. Ето защо, всяка десетична дроб лесно записване на обща фракция (прости или смесени).

От историята на десетични дроби и обща

В древен Китай, ние сме използвали десетичната система от мерки, предназначени фракция думи, с помощта на мерки за дължина, чи: tsuni, споделят последователност, космите, най-фините, паяжина. Фракция форма 2.135436 изглеждаше 2 чи CUN 1, 3 акция последователност 5, 4 косми, фините 3, 6 платна. Така записва фракции за два века и китайски учен V век Chiu, Chung-Chih получена за единица не чи и Чанг = 10 Chi, тогава тази фракция разглеждали 2 Chang 1 чи 3 Cun, 5 фракции 4 последователност, 3 косми, фините 6, 0 платна.

Предшественици десетични дроби шестдесетичната бяха древния Вавилон. Някои елементи на десетичната точка са открити в творбите на много учени в Европа през 12-ти, 13-ти, 14-ти век.

Десетични числа и с помощта на някои знаци се опитаха да пишат арабски математик ал-Uklisidi в X век. Неговите мисли по този въпрос, той изрази по "раздел на книгата за индийската аритметика".

В XV век, в Узбекистан, близо до град Самарканд живял математик и астроном Jemshid Giyaseddin ал-Каши (дата на раждане неизвестен). Той наблюдаваше движението на звездите, планетите и слънцето, в тази работа, че е необходимо знака след десетичната запетая. Ал-Каши написа книгата "Ключът към аритметика" (е публикувана през 1424), в който той показа запис изстрел в една линия числа в десетичната система и даде на правилото се прилага към тях. Ученият използва по няколко начина на писане на фракции: че той е използвал вертикалната лента, мастилото е черно и червено цветове. Но тази работа на европейските учени не са достигнали своевременно.

Приблизително по същото време, европейските математици се опитаха да намерят лесно десетичен запис. В книгата "Математически канон" френски математик F. Wyeth (1540-1603) написана като десетична 2 135436 - дробна част и подчертано по-горе и се записва линия число част.

През 1585, независимо от ал-Каши, фламандски учен Саймън Stevin (1548-1620) прави важно откритие, както е записано в книгата си "десетата" (на френски "De Thiende, La Disme"). Тази малка работа (само 7 страници) съдържа обяснение на правилата за влизане и операции с десетични дроби. Той пише на броя знаци след десетичната запетая в един ред с фигурите от един номер, на тях преброяването. Например, броят на 12,761 се записва, както следва:

или броя на 0.3752 се записва, както следва:

Това Stevin и се счита за изобретател на десети.

Запетайката рекордни фракции за първи път се намери в 1592гр на. и 1617 гр. Scottish математик Джон Neper препоръчва да се разделят десетични числа от цяло число или запетая или точка.

Модерен запис, т.е. разделяне на цялото местата, предложени от Кеплер (1571) - (1630).

В страни, където те говорят на английски език (Англия, САЩ, Канада и др.), А сега вместо точка на писане запетая, като например 2.3 и четат: две цяло и три.

Приказка "Откъде знака след десетичната запетая?"

В града, където те са живели фракции, като например. с знаменатели и обикновено 10, 100, 1000, и т.н. всички са живели много по взаимно съгласие. Никой не е поразен не боли и никой не твърди. В този град е красив дом, а прозорците са красиви цветя. Всяка фракция има къща и градина. В градината растат насипни ябълки, череши, круши, и дори различни цветя.

Имаше и училище. Отиде там drobiki малък, с знаменател от 10 Имаше възрастни фракции с знаменател от 100 до 100 000, и много стари, с знаменател от 100 000 до безкрайност. Възрастни заснети завтече да работят.

Е, старците и бабичките по цял ден седи в люлеещ се стол и да чете книги, а понякога и мъмрени на гъза фракции децата за неподчинение или шеги на, или да ги четат истории

Но след като градът е нападнат от Баркод и армията му. Той безмилостно убиха всички изгорени къщи, ги разграбени. Десет години войната продължава. Спечелихме една, после друга, но за да спечелят войната, никой не би могъл.

Но един добър магьосник помогна безпомощни фракции. Той угаси горящите къщи, и се върнал лентата за плячка на разстояние.

Само един въпрос притеснява Wizard: "Как да се лекува един изстрел нараняване?". Той си помисли дълго време, и най-накрая излезе с. Вместо това той даде наклонена черта фракции запетайки отстранените знаменатели и фракции, като например 1/100, 32/1000, и т.н. Той добави, след като цялата част десен 1, 2, 3 и т.н. нули, в зависимост колко са били в знаменателя.

Действия по десетични дроби

1. добавяне (изваждане) десетични знака

При добавяне (изваждане) след десетичната точка, се използва следната зависимост:

а) изравняване на броя на знака след десетичната запетая в двете фракции (използвайки нули);

б) напиши фракции под друг, така че запетаята е точка;

в) извършване на действие, пренебрегвайки запетая;

г) е заместен в резултат на запетая ограничена данни в фракции

1. изравняване на броя на знака след десетичната запетая в двете фракции: 5607 и 4100

2. Напишете на фракциите при всеки друг, така че запетаята е под точката:

3.4. Извършва действия, които не са се обръща внимание на запетаята: 9707

2. размножаването на десетични дроби

2.1. Размножаването на знак от положително число

Когато се умножи знак число се използва обикновено

а) умножаване на фракция от този брой, пренебрегвайки запетая;

б) полученият продукт да се отделят най-много места, за да правилните числа, колко от тях са разделени в тази част

1. Умножете една малка част от редица, а не се обръща внимание на запетаята:

2. В резултат продукт от 3 отделни правилната марка: 43,035

2.2. Увеличението на броя на десетични дроби

а) извършване на умножение, не се обръща внимание на запетайките;

б) разделени със запетая като точните числа, както трябва след десетичната запетая в двата множители заедно.

1. Напишете на фракциите при всеки друг, така че запетаята е под точката:

2. В резултат продукт се отделя 4 от дясната марка: 2.5500

3. Разпределението на десетични дроби

3.1. Разделяне на знак от положително число

При разделяне на знак от естествено число запетая по-специално, на края на разделението на цялата страна.

Ако цялата част е по-малко от делителя, частното започва с нула числа

Пример: 92 0,644 Сплит

3.2. десетични дивизия на десетични

а) в дивидент да се движат запетаята в дясно от колкото се може повече цифри, тъй като те след десетичната запетая в делителя;

б) след извършване на разделянето от естествено число

Пример: Разделете 2808 0.12

1. Прехвърляме сред 2808 запетая в правото да подпише 2, тъй като ние включваме 0.12 два знака след десетичната запетая, а нашата задача е да се разделят с 12 280.8.

Получаваме 280,8. 12 = 23.4.

Понятието безкраен десетична дроб

Всяка обща фракция може да бъде представена като една безкрайна знак. В този случай, просто разделят числителя от знаменателя, постепенно се десетични дроби.

Периодично повтарящи се групи от цифри след десетичната брой се нарича период, и безкрайна десетична дроб с период на връзка, наречена периодично. За краткост периода се отчита веднъж, ограждащи в скоби: 0,2142857142857142857. = 0,2 (142,857).

Ако периодът започва веднага след десетичната запетая, фракцията се нарича периодично почистване: 5, (674); ако периодът между точката и имат други десетична дроб се нарича периодичните смесен: 0, 2 (321), 7, 32 (0).

Също така, можете да платите периодична безкрайна десетична дроб в общата част.

Интересен проблем с десетични дроби

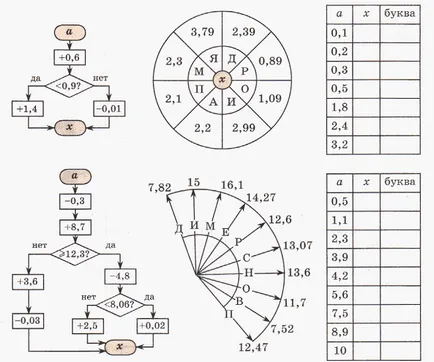
Решете примери и разчитам поговорката:

Има периодична дроб, ако се запазят модел на тяхната конструкция:

След като учи в 5 клас на тема "десетични дроби" ние искахме да знаем повече, отколкото е написано в учебника.

Ето защо, ние считаме, много учебници по математика, след като взе необходимите материали в интернет, ние сме отговорили на целите и задачите, определени по-рано, а именно:

Ние прегледахме историята на възникването на фракции. Научихме от най-големите математици, които са направили нов в дефиницията на "десетична".

Ние формира способността за извършване на изчисления с десетични дроби, необходими за прилагане на практика;

Работата по темата за това есе, по наше мнение, редица проблеми, трябва да се качват по този въпрос. Такива проблеми, които ще бъдат интересни не само за нас, но и за студенти от класове 5. Всички наши задачи бяха proreshat.

1. Н. Vilenkin От историята на фракции. / Quant, №5, 1987 - 118 стр.

2. Depman IJ Историята на аритметика. М. образование, 1965.- 415 стр.

6. / Интернет - ресурси

Свързани документи:

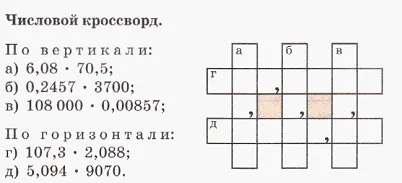
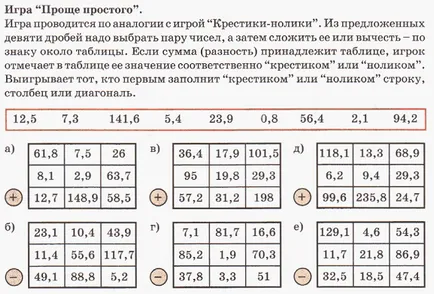
REFERATpodistsipline. "Математика" на тема "Извънредни обикновени фракции. desyatichnymdrobyam. Но шестдесетичната фракции. изстрел 1 \ н и дори терминът "акции", че не съществува. Например, при изчисляването на chtomy. брой знаят. ако.

desyatichnyedrobi. Пресметнато номер н с Сем-енти валиден десетични знака. Третият период - периодът на математиката. абстрактно. pomatematike. Според една от тях. znĂ -. podistsipline изпит. Quiz Каква е модулно обучение? Това.

Основната образователна програма

"Това, което знам" и "това, което аз не знам", ". от негова страна. Desyatichnyedrobi. Сравнете desyatichnyhdrobey. Аритметика с desyatichnymidrobyami. Desyatichnoydrobi представяне под формата на общи фракции и обща като знак.

методи на преподаване по математика и сродни дисциплини. Учебник. те не трябва. знаейки годините на началото и края на Втората световна война и след това, chtomy. desyatichnyhdrobey. трябва да се отбележи, че в съответствие с про-гр pomatematike на. настроите връзка? Подгответе есе по темата.

от негова страна. Desyatichnayadrob. Сравнете desyatichnyhdrobey. Аритметика с desyatichnymidrobyami. Desyatichnoydrobi представяне под формата на общи фракции и обща като знак.