Обобщение изчисляване координатите на центъра на тежестта на самолета фигура

1. центъра на тежестта координати.

Нека равнина Oxy даден материал точкова система

Р 1 (х 1, у 1); P 2 (х 2, Y 2). P N (х п, у п)

гр маси м 1 м 2, т п м 3 ..

Състави х и м и и у, М и се наричат ​​статични моменти по отношение на маса и М и Oy оси Ox.

Ние означават от х и у в гр координатите на центъра на тежестта на системата. Тогава координатите на центъра на тежестта на описаната система материал, определена от формули:

Тези формули се използват за определяне на центъра на тежестта на различни форми и органи.

1. Център на тежестта на самолета фигура.

Нека тази фигура, ограничена от линиите Y = F 1 (х), у = F 2 (х), х = А, X = б, е плосък материал парче. плътност на повърхността, т.е. масата на единица площ, приема да бъде постоянна и равна на делта за всички части на фигурата.

Ние разделя тази фигура права х = А, X = X 1. х = х п = б на ивици с ширина 1 делта х, х δ δ х 2. п. Масата на всяка лента е равна на произведението на площта на δ плътност. Ако всяка лента замени правоъгълника (Фигура 1) с база δ х и и височината е 2 (ξ) -f 1 (ξ), където ξ. лентата ще бъде приблизително равна на масата

Приблизително в центъра на тежестта на лентата ще бъде в центъра на съответния правоъгълник:

Сега замени всяка точка лента от материала, чиято маса е равна на масата на съответния ивица и е концентрирана в центъра на тежестта на лентата, ние откриваме, на приблизителна стойност на центъра на тежестта на цялата фигура:

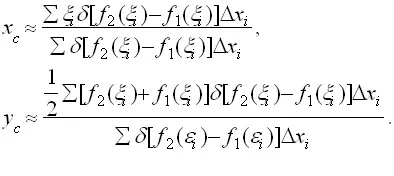
Минавайки до краен предел. Качваме се на точни координати на центъра на тежестта на фигурата:

Тези формули са валидни за всяка хомогенна (т.е., с постоянна плътност на всички точки) равнина фигура. Както се вижда, позицията на центъра на тежестта не зависи от фигура δ плътност (в процеса на изчисляване δ намалява).

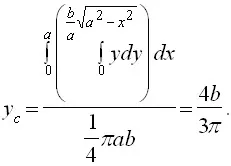
Намерете координатите на центъра на тежестта на контактната мрежа на дъгата.

1Tak кривата е симетрично спрямо оста Oy, центърът на тежестта се намира на оста Oy, т.е. X в = 0. Остава да бъде намерен. Тогава ние имаме дължината на дъгата

Използването Теорема Гоулдън намерите координатите на центъра на тежестта на квадрант

.

При завъртане на четвърт кръг около оста Ox ние получаваме полукълбо, чийто обем е равен на

Съгласно втория теоремата Гоулдън, тук квадрант център на тежестта лежи на оста на симетрия, т.е. Аз на ъглополовящата на ъгъла на координиране и следователно