низ вибрации
Цел: проучване на вълна явления, условията за съществуване на стоящи вълни, изучаването на еластичните свойства на низа.
Основната теоретичния
Нека точка се люлее, тя се намира в среда, в която са свързани всички частици. Тогава енергията на вибрациите може да се предава около точката на точки, предизвиквайки своите люлки. Феноменът на разпространение на вибрации в среда, наречена вълна. В този колебания частици не се движат с проникващ осцилаторна процеса, и се колебаят около техни равновесни позиции.
Ако свободно да се разпространява нито една вълна безкрайно среда, тя се нарича бягаща пътека. Ние се образува уравнението на вълната пътуване, която позволява да се определи преместването на всяка точка на вълните по всяко време.
Фиг. 9.1. За да се извлече уравнение на бягаща вълна
Нека разгледаме непрекъсната еднородна среда
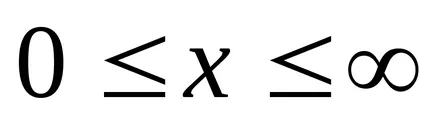

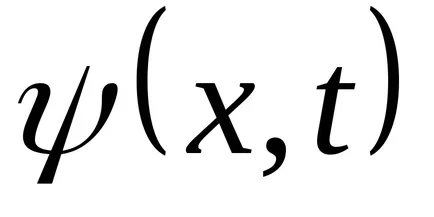
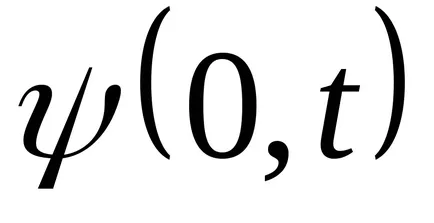


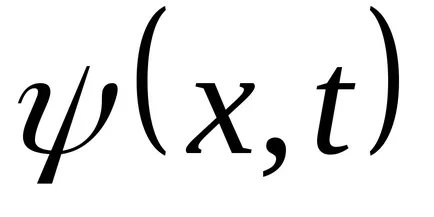
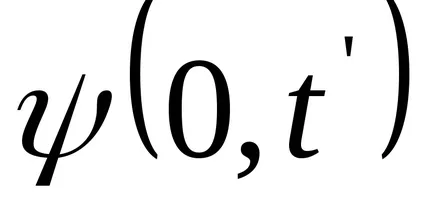


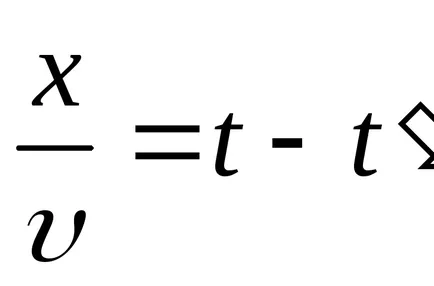
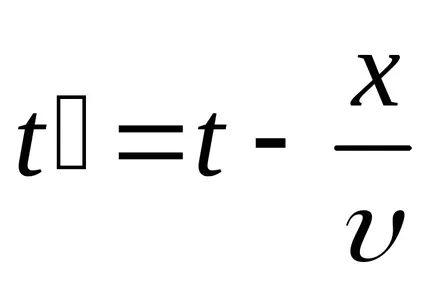
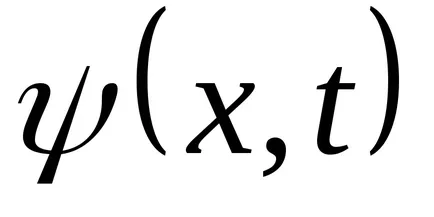
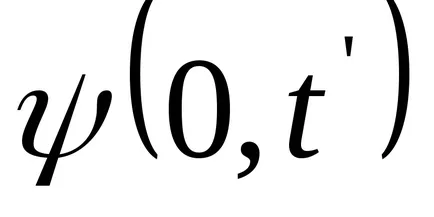

Transform функция (9.1):
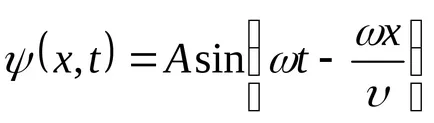
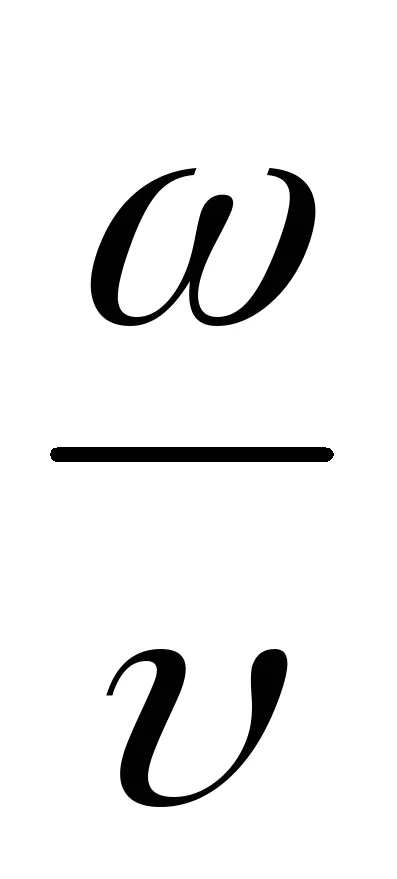
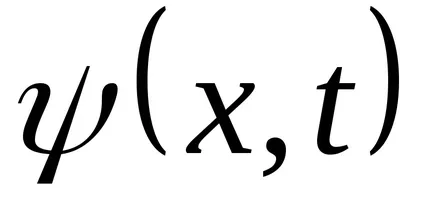
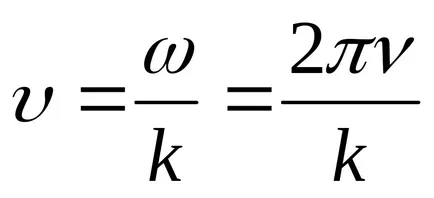


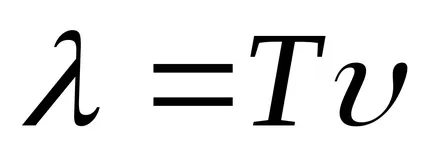
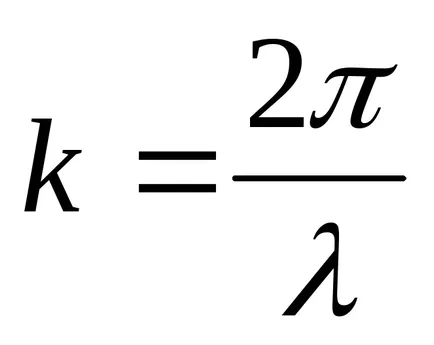
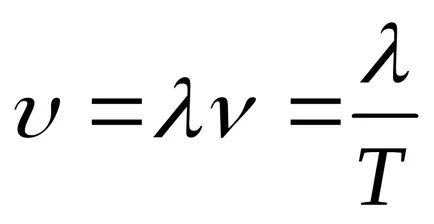
Уравнение (9.1) е уравнението на вълните пътуване измерения (или плоски). За дадена х е да се определи позицията на точка (и равновесие позиция координира X) в даден момент т. За даден тон позволява определяне на моментната позиция на осцилиращи точки.
По този начин, ние виждаме, че движението на вълната има двойно честота. От една страна, всяка частица на средата се подлага на периодично движение във времето, от друга страна, при всяка точка от време, всички частици се поставя на линията, която форма се повтаря периодично в пространството.
Ние дефинираме скоростта размножаване на надлъжните вибрациите по демон-течение на дълъг прът с постоянно напречно сечение.
Фиг. 9.2. Размножаване на еластична деформация по прът
rideystvii в лявата част на сила

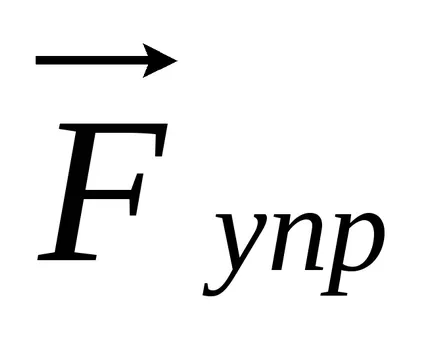
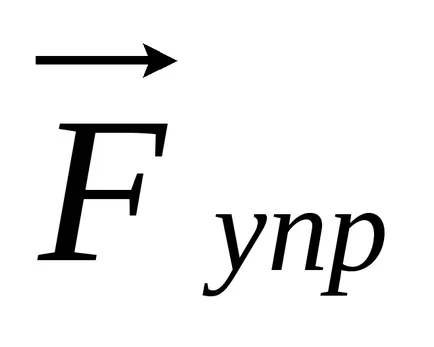

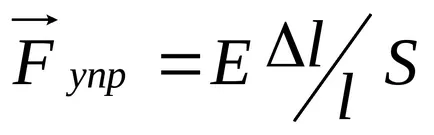

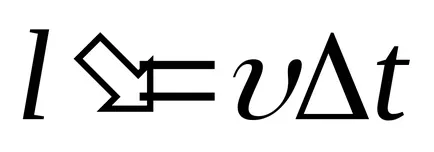
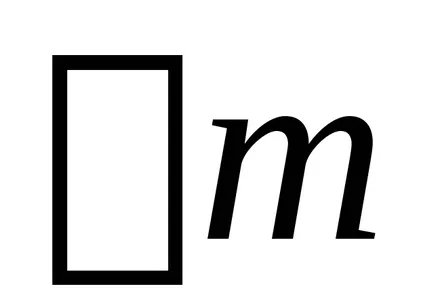
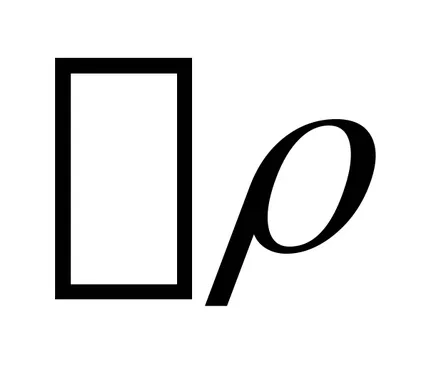
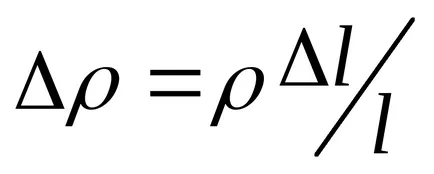
където
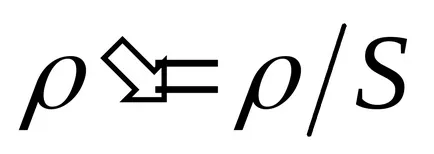
Уравнение (9.1) описва една вълна посадъчен в положителната посока на оста на г-н О. При смяна на посоката на разпространение на вълната за противоположния втори мандат в аргумента на косинус променя знак, тъй като

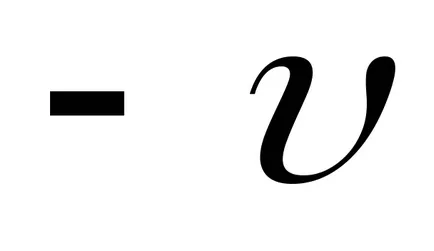
Помислете сега разпространение на вълни в низ фиксирани в двата края. В тази вълна, движещи се в една посока, след като е достигнал втори фиксиран край на веригата и ще се разпространи отразено в обратната посока. По този начин по дължината на вълните на низови възникне наслагване явление посадъчен в противоположни посоки. Ако свойствата на течност не се променят под въздействието на вълната размножителен, принципът на наслагване се извършва, като всяка вълна размножени в средата независимо от другите. В този случай полученият изместване Z на средни частици се определя като количеството на изместване Z1 и Z2. причинени от преминаването на отделните вълни. В резултат на това тя ще се появи в различни точки на средна печалба или затихване на трептенията в зависимост от влизането смущение фаза.
Присъединителните вълни, където в различни точки на средата са оформени на амплификация и затихване на трептенията амплитуда се нарича смущения вълни. Това смущение модел се поддържа в течение на времето.
Помислете за намесата на две вълни с еднаква амплитуда пътуват в противоположни посоки, като в случай на низ фиксирани в двата края. Необходимо е да се вземе предвид следното явление. След отразяване от фиксирания край отразява деформация има обратен знак. Това е разбираемо като се има предвид, че тъй като изместването на фиксиран край през цялото време отсъства от точката на закрепване на силите, противопоставящи се на входящо низ огъване. Тези сили генерират огъване на обратен знак, започва да се разпространява в обратната посока. Ето защо, деформация в отразена пристрастия знак да се отпише. Ако отразено хармонична вълна, подобна промяна е равносилно на "загуба" половин вълна на размисъл.
По този начин, суперпозиция на две вълни дава следното:
.
Използването на разликата на Синиш формулата, получаваме
Този израз се нарича уравнение на стояща вълна, като се предполага стационарни трептения, т.е. режим, която се проявява след многократни вълни се движат между автомати низ. От (9.4) ние виждаме, че в средата на стояща вълна всички точки (всяка стойност на х) варира синусоидално с ъглова честота .
Амплитудата на колебание е различен за различните точки и се определя от (9,4), както следва:
От последния израз следва, че има точка на средата, наречени възли, в които няма колебания ZM = 0, по този начин, Z = 0. Координатите на тези точки се определят от условието, че синус в (9.5), т.е.
Следователно, тъй като
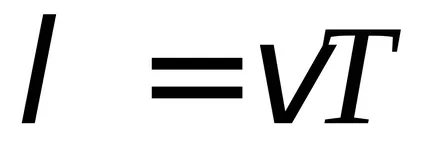
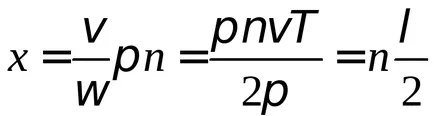
Следователно, разстоянието между съседни възлови точки е равна на половината от дължината на вълната. Тъй възли по всяко време остават в покой, постоянната вълна не е насочено пренос на енергия, енергията не може да премине през възела. Прехвърлянето на енергия по протежение на низа е само на бягаща вълна.
Тези точки, в които амплитудата стойност достига максимум

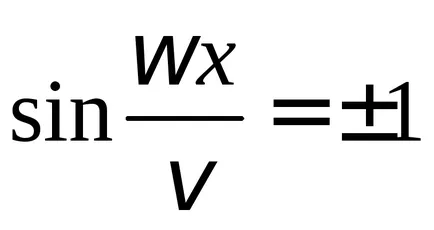
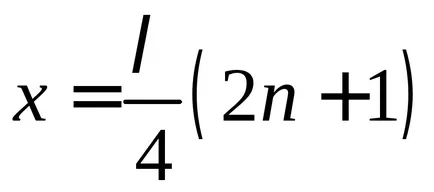
фактор
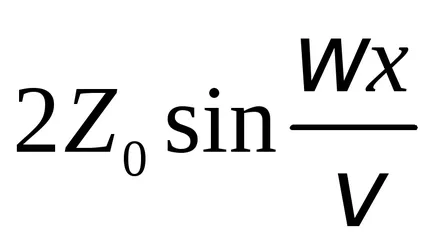
По този начин, стояща вълна се образува само когато подходящ размер съотношението низ и дължина на вълната (честота на трептене). За различни стойности на п = 1, 2, ... ние получат различни видове или видове колебания, където п определя броя на antinodes и не възли. От (9.6) с (9.7) получаваме израз за честотите, на които са установени стоящи вълни в низа
честоти
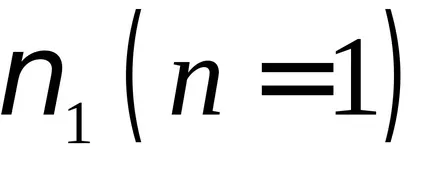
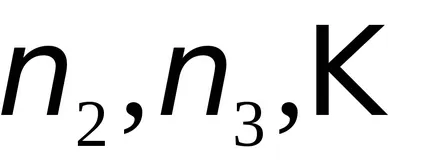
Като цяло, в вибрациите низ може да съществува с различни естествени честоти. Така, заедно с основния тон на п = 1, може да бъде възбудени нюанси п = 2, 3, 4, ....
Получени по-горе уравнения описват движение напълно гъвкав низ във вакуум. Когато вибрациите на низа е винаги една истинска енергийна възникнат загуби.
Част от енергията се губи поради въздух триене, от друга страна преминава през краищата на низа и т.н. За да се поддържа незатихващи трептения е вибратор. Ако загубата на енергия в точност се компенсира от енергията, идваща от вибратор, низ може да се види стоящи вълни. Но сега, низа трябва да е предаване на енергия. Ето защо, пътуващи вълни ще съществуват заедно със състояние, в резултат на което някои от тях да бъдат замъглени. Ако загубите на енергия за периода са малки в сравнение с предлагането на вибрационната енергия в низа, изкривяването на туриз вълна стояща вълна ще бъде незначително.
Друг подход към по-горе теория е небрежност низ хетерогенност. В истински струнни и плътност, както и напрежението може да бъде непрекъснатост на координатите на X. Например, ако низът е спряно вертикално, теглото на сметката на низ ще доведе до факта, че напрежението в горната част е по-голяма от дъното. Всяко нехомогенност ще доведе до нарушаване на вълната на сигнала, тъй като синусоидална трептенията в пространството на само характеристика на обичайните начини на хомогенни системи.