Нехомогенни линейни диференциални уравнения с произволни коефициенти
Да разгледаме уравнението на формата
С отбелязването можем да запишем:
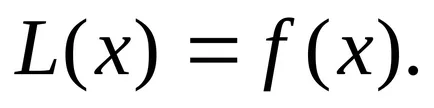
В този случай ние приемаме, че коефициентите и от дясната страна на това уравнение са непрекъснати в някакъв интервал (краен или безкраен).
Teorema.Obschee разтвор на нехомогенни линеен диференциално уравнение в регион, е сумата от всички решения и общото решение на съответния хомогенна линейна диференциално уравнение.
Доказателство. Нека Y - разтвор на нехомогенни уравнението.
След това чрез заместване на този разтвор в оригиналния уравнение получаваме самоличността:
нека
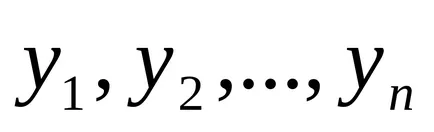
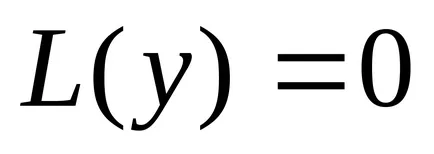
Следваща ние показваме, че сумата от общото решение на нехомогенни уравнението.

Общо казано, разтвор Y може да бъде получена от общия разтвор, защото Това е специално разтвор.
По този начин, в съответствие с настоящото теоремата за решаване на линеен нехомогенни диференциално уравнение трябва да се намери общ разтвор на съответните уравнения хомогенни и по някакъв начин да се намери специално разтвор на нехомогенни уравнение. Обикновено това е избора.
Той е удобен за използване на метода на вариация на произволни константи.
За тази цел първо намери общ разтвор на съответното хомогенно уравнение под формата:
След това, ако се приеме koeffitsientyCifunktsiyami crushi, ние търсим решение на нехомогенни уравнение:
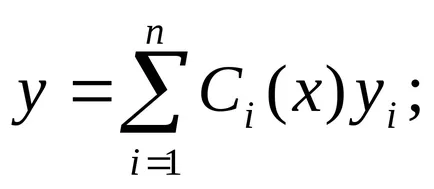
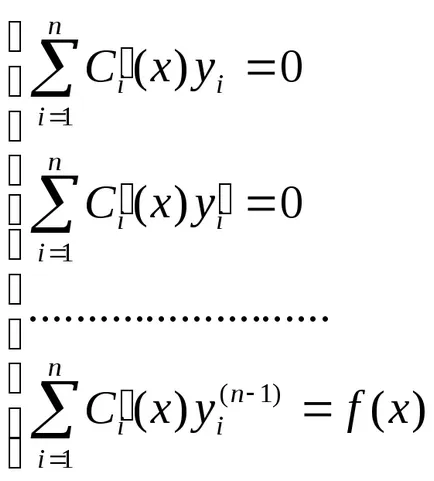
Пример. решаване на уравнението
Решаването на хомогенна линейно уравнение
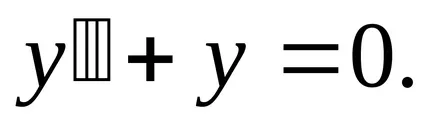
Решението на нехомогенни уравнението ще изглежда така:
Представлява система от уравнения:
Ние решаваме тази система:
От отношението намерите funktsiyuA (х).
Сега ние намерите B (х).
Замести стойностите, получени в общия разтвор на нехомогенни уравнение формула:
Така, че е възможно да се избегне намиране на конкретно решение на нехомогенни уравнението на пробата и грешката.
Общо казано, методът на вариация на произволни константи подходящи за намиране на решения за всяка линейна нехомогенни уравнение. Но тъй като намиране на основното система на разтвори на съответното хомогенно уравнение може да бъде доста предизвикателство, този метод се прилага главно за нехомогенни уравнения с постоянни коефициенти.
Нехомогенни линейни диференциални уравнения с постоянна
Уравнението с дясната страна на специален вид.
Възможно е да си представим, под формата на конкретно решение в зависимост от вида на дясната страна на нехомогенни уравнението.
Има следните случаи:
I. В дясната страна на нехомогенни линеен диференциално уравнение има формата:
където - полином stepenim.
След това се търси конкретно решение под формата на:
Тук, Q (х) - полином от същата степен като Р (х). но с неопределени коефициенти и R - редица показва колко пъти брой е корен на уравнението характеристика за съответната хомогенна линейна диференциално уравнение.
Пример. решаване на уравнението
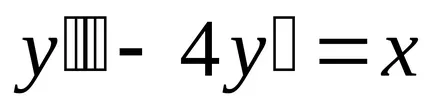
Ние решаваме съответното хомогенно уравнение:
Сега ние откриваме конкретно решение на оригиналния нехомогенно уравнение.
Нека сравним дясното изложение дясната страна, по-горе.
Конкретният решение се търси във формата, където
Сега ние определяме неизвестните коефициентите А и Б.
Заместването конкретен разтвор в обща форма в първоначалния нехомогенни диференциално уравнение.
Общо частично решение:
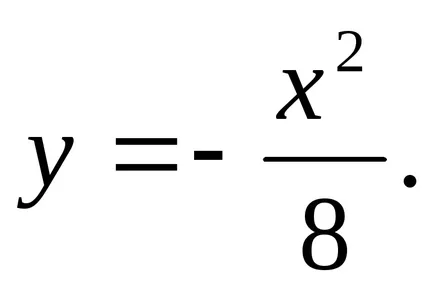
След това общото решение на нехомогенни линеен диференциално уравнение:
II. Дясната страна на нехомогенни линеен диференциално уравнение има формата:
След това конкретно решение на уравнението нехомогенни ще изглежда така:
където броят на R показва колко пъти на броя на
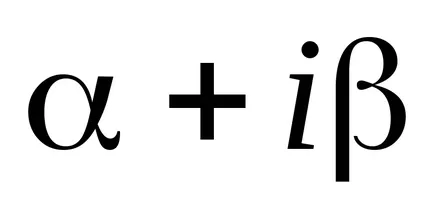
Забележете, че ако дясната страна на уравнение е комбинация от изразяване на обсъдено по-горе тип, разтворът е комбинация от разтвори на помощни уравнения, всеки от които е от дясната страна съответстваща на експресия на комбинацията.
Т.е. ако уравнението е от формата, след това конкретно решение на това уравнение е
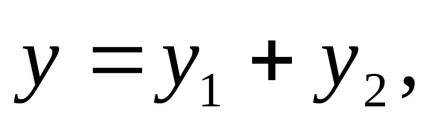
За да се илюстрира пример решаване друг метод по-горе.
Пример. решаване на уравнението
Състав и решаване на характеристика уравнение: