Начин на прости повторения
Методът е прост повторения в изчисляването на новата точка х на стария точка.
Итерацията продължава, докато желаната точност разтвор епсилон.
[Редактиране] решение алгоритъм
Вход: A, B, ε.
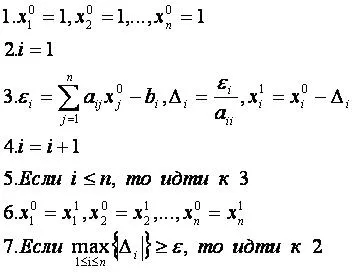
Изход: х.
За решения от прости повторения на линейни уравнения Ах = б система (където А - NxN квадратна матрица на коефициентите, и б - вектор свободни членове на системата), първо намери основната система детерминанта Δ.
Метод на прости повторения се прилага (т.е. метод конвергентна), ако основната детерминанта на системата Δ ≠ 0 и условията на един от два случая:
1), когато поне един от нормите на матрица В = E-A е по-малко от 1:
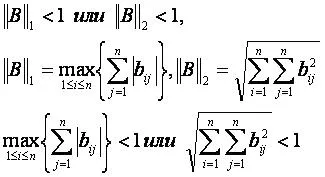
2) когато всички собствените стойности на матрицата В = Е-модул по-малко от 1.
За да проверите условията на втория случай е необходимо да се определи стойност λ = max1 |, | λ2 |, ..., | λn |>. където λ1, λ2, ..., λn - собствени стойности на Б. и проверка на състоянието ДълЖината<1 .
Обикновено, матрица В = Е-А отговаря на горните условия, когато основният диагонала на матрицата А са доминиращи елементи на ангиотензин II;
Aii доминиращ елемент е задоволяване на неравенството елемента: