на въздействието

При сблъсък на кинетичната енергия на органите, на които те са имали преди удара, частично или напълно се превръща в еластична енергия и на вътрешната енергия на телата.

Има две крайни случаи на шок: напълно еластични и нееластични абсолютно. Той призова абсолютно еластичен удар, при който механичната енергия на тялото не навлиза в други форми на енергия. Когато такъв сблъсък кинетичната енергия се преобразува изцяло или частично в потенциална енергия на еластичната деформация. След това тялото се връща в първоначалната си форма, бутане един на друг, както и потенциалната енергия се превръща в кинетична отново, тялото и лети със скорост, определени от законите на запазване на енергията и инерция.

Напълно нееластично въздействие се характеризира с това, че потенциалната енергия на деформация не възниква. Кинетичната енергия на органи напълно или частично се превръща в вътрешна енергия. След удара тялото пред които са изправени, преместете заедно или в покой. Когато такъв сблъсък закона за запазване на инерцията, не се изпълнява закона за запазване на механичната енергия.

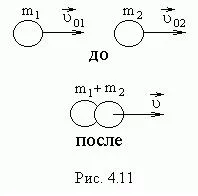
Да разгледаме напълно нееластично сблъсък на две частици (масови точки), които образуват затворена система (фиг. 4.11). Тежести частици. тяхната скорост преди удара, и. След въздействие, скоростта на частиците са еднакви и равни. Според закона за запазване на инерцията, ние имаме:

Тогава скоростта на частиците след удара.

А сега да разгледаме абсолютно еластична въздействие, като ограничи до централната въздействието на две хомогенни сфери. Strike нарича централна ако на стачка топките се движат по права линия, преминаваща през техните центрове. Когато може да се случи централната сблъсък въздействие, ако топките се движат един към друг (фиг. 4.12), или някой от другите топки улова (ris.4.13).

Ние приемаме, че топките образуват затворена система и няма въртене на топки.

Масови топки и. тяхната скорост преди удара, и. След удря тяхната скорост и. Според закона за запазване на енергията

според закона за запазване на инерцията. (4.16)

Произведението на уравнение (4.15) и група 2, получаваме :. или от (4.16)

Разделяне първият от тези уравнения за втория

Увеличаването (4.18) и да се изважда от резултата (4.17)

От изразите (4.19) показва, че скоростта, след като удари топки може да не са идентични. Наистина, което се равнява и. = Получите. т.е. топки скорости трябва да са идентични и да духат, но в този случай не може да се случи на сблъсъка.

Да разгледаме случая, когато масите на сблъскващи топки са равни. Така, както следва от (4.19). т.е. топки в лицето валутните курсове.

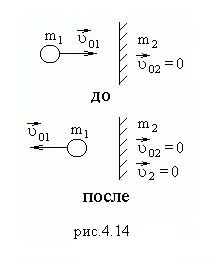
При разглеждане на съвършено еластично сблъсък топката на стационарни или движещи се стени, за да се види, като последния топката на безкрайна маса. След разделяне на числителя и знаменателя на (4.19) до (стена маса) и поемане 0, ние получаваме.

Ако стената е фиксиран (ris.4.14) = 0, скорост на топката променя своята посока, скорост модул остава непроменена.