На теоремата на площта на ортогонална проекция - геометрия, правоъгълна тетраедрите

Нека разгледаме формулата на правоъгълни прожекционни лица на тетраедър. Предварително помислете правоъгълната проекция сегмент лежи в равнината α. подчертаване два случая местоположението на сегмент спрямо линия L = α∩π.
Дело 1.AB # 8741; л (фигура 8.). Сегмент А1 В1. е правоъгълната проекция на сегмента AB, и е успоредна на сегмента AB.

случай 2.CD⊥l (фиг. 8). По теоремата на три вертикалите права С1 D1. е ортогонална проекция линия CD, също перпендикулярна линия л. Следователно ∠CEC1 - ъгълът между алфа самолета и прогнози равнина π. т. е., когато С0 D = С1 D1. Затова | C1 D1 | = | CD | # 8729; защото
Сега ще обсъдим въпроса за проектиране ортогонална триъгълник.
Площта на ортогонална проекция върху равнината на триъгълника е равно на проектираната площ на триъгълника, умножена по косинус на ъгъла между триъгълна равнина и равнината на проектиране.

Доказателство. Площта на проекцията на триъгълник.
а) Ако една от страните, като АС, очаква триъгълник ABC е успоредна линия L = α∩π (фиг. 9) или лежи върху него.

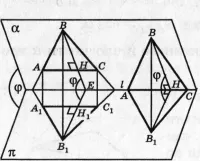
Тогава височината BH е перпендикулярна на линията л. а районът е равен, т.е.. д.

Въз основа на по-горе обсъжданите свойства на ортогонална проекция на сегмента са:

По теоремата на три вертикалите директно В1 Н1 - ортогонална проекция на права линия HV - перпендикулярна на линия L, следователно, сегмент В1 Н1 - височина триъгълник А1 В1 С1. Ето защо. По този начин.
б) Нито една от страните на проектираното триъгълника ABC не е успоредна на линията L прави (фиг. 10). Чрез всеки връх на триъгълник линия, успоредна на линията л. Един от тези прави линии е между другите две (на фигурата - е директна т), и по този начин разделя ABC триъгълник триъгълници АБД и ACD с повишения съответно ВН и CE проведени тяхната обща страна AD (или разширение), която е успоредна на л. Директен m1 - правоъгълната проекция на линия M - също разделя триъгълник А1 В1 С1 - правоъгълната проекция на триъгълник ABC - триъгълници А1 В1 и А1 D1 С1 D1. къде. Като се има предвид (9) и (10), получавайки

По този начин, за произволно разположени в триъгълник ABC α равнина се осъществява