метод Кал за решаване на задачи на линейното програмиране

Най-простият и най-очевидна метода на линейното програмиране (LP) е графичен метод. Той се използва за решаване на проблемите LP с две променливи.

Помислете за проблема с LP в стандартна нотация:

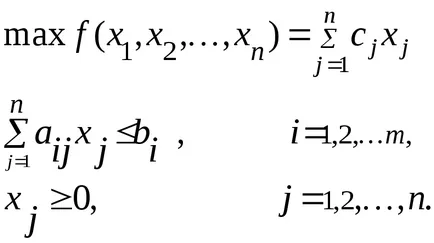
Нека п = 2. т.е. разгледа този проблем в самолета. Нека системата на неравенството съвместим (има поне едно решение).

Всяка неравенството на системата геометрично определя полуравнина с гранична линия ai1x1 + ai2x2 = BI. I = 1,2, ... m. nonnegativeness условия определят половината равнина, съответно, с гранични линии x1 = 0, Х2 = 0. системата е последователно, така че половината равнина като изпъкнали комплекти пресичат, образуват обща част, която е изпъкнала и множество е набор от точки, координатите на всяка от които са решение за тази система. Съвкупността от тези точки се нарича полигон решения. Тя може да бъде точка, сегмент, лъч, многоъгълник, неограничен многоъгълна област.

Така геометрично линейното програмиране проблем (ZLP) представлява намирането на точка на разтвори многоъгълник, който координира достави линеен цел функция максимум (минимум), при което стойността на допустимите разтвори са разтвори на всички точки на многоъгълника.

Линейно уравнение описва множеството от точки, лежащи на една права линия. Линейно неравенство описва определена област на самолета. Определя коя част от равнина, описана от 2x1 неравенството + 3h212. Първо, ние изгради права 2x1 + 3x2 = 12. Тази линия минава през точката (6, 0) и (0, 4). За да се определи коя половина самолет удовлетворява трябва да изберете някоя точка от графиката, не е собственост, пряко, и да замени нейните координати в неравенството. Ако неравенство притежава, а след това тази точка е осъществимо решение, както и полу-равнина, съдържаща точка удовлетворява

неравенство. Подходящ за използване, когато заместен в неравенството е произхода. Заместител Х1 = Х2 = 0 в неравенството 2x1 + 3h212. Ние получи 20 + 3012. Това твърдение е истина, следователно неравенство 2x1 + 3x2 12 съответства на долната половина на равнината, съдържаща точката (0,0). Това е отразено в графиката, показана на фигура 1.

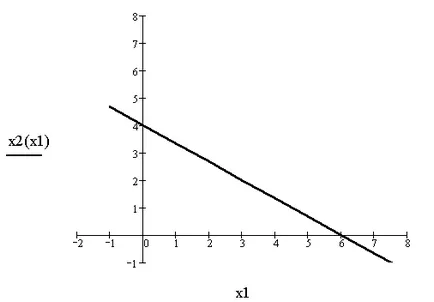
Фиг. 1. неравенство 2x1 + 3x2 12 съответства на долната половина равнина.

По същия начин, можете графично всяка ограничаваща линейното програмиране проблем.

Решение всяка система ZLP неравенство ограничения е полу-равнина, съдържаща гранична линия и са разположени от едната страна на него. Пресечната точка на половин равнини, всеки от които се определя от съответния неравенството на системата, наречена домен на възможни решения или домейн. Трябва да се помни, че площта на изпълними решения задоволяване

nonnegativeness условия (XJ 0, J = 1, ..., N). Координатите на всяка точка, която принадлежи към областта на определение е валидно решение на проблема.

За стойността Екстремален на обективната функция, когато нанася решаване на проблемите LP използвайки градиент вектор, координатите на които са частични производни на обективната функция, т.е.

.

Този вектор показва посоката на най-стръмната промяна Цзе-ляво функция. Права линия, перпендикулярна на вектора градиент е нивото на линия на обективната функция. Във всеки един момент ниво линия обективна функция е на същата стойност. Ние приравняваме стойността на целевата функция на постоянна "А". Промяна на стойността на "а". Ние се получи семейство от успоредни линии, всяка от които е нивото на линия.

Важно свойство на линейна функция на линията на ниво е, че паралелно движение на линията само в една посока повишава нивото, докато изместване в другата посока - намалява.

От геометрична гледна точка, задачата на линейното програмиране се търси такава точка ъгъла или набор от точки на възможен набор от решения, което се постига чрез най-горната (по-ниска) ниво линия, разположен на (в близост) в друга посока на най-стръмната растеж.

Графично разтвор метод ZLP се състои от следните етапи.

Построен многоъгълна площ от осъществимо решения ZLP - SDT,

Вграден градиент вектор СР в някакъв момент X0 принадлежи SDT -

.

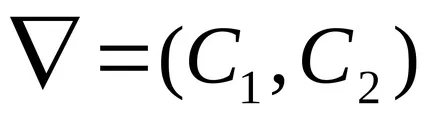
ниво 3. Линия C1x1 + C2x2 = а (а е постоянна стойност) - линия, перпендикулярна на вектор градиент

- се движи в посоката на вектора в случай maksimizatsiif на (x1, x2) доколкото листата извън SDT. Резерв точка (или точки) на региона с движение и точка на максималната е (х1, х2).

4. За да открият произхода му е достатъчно за решаване на две уравнения на линиите, получени от съответните ограничения и даване в точката на пресичане на максимум. Стойността на F (х1, х2), намерено в получената точка е максимум.

В минимизиране е (х1, х2) ниво линия се движи в обратна посока на вектора на градиент. Ако една права линия, докато се движи не оставя SDT, съответната максимална или минимална на F (x1, x2), не съществува.

Ако нивото на линия, успоредна на всяка функционална проблем ограничение на оптимална DF стойност ще бъде постигнато във всяка точка на това ограничение, разположена между две ъглови точки оптимално, и следователно, всеки от тези точки е оптимално решение ZLP.

Помислете за графично решаване на задачи на линейното програмиране със следния пример.