Math 1 (17)

1. Намерете неопределен интеграл (табл. 1).

а) е неразделна като сума от интегралите, първият от които се интегрира директно, а втората са представени в таблицата:

б) преобразуване на подинтегрален се използва формулата на двоен ъгъл и да се интегрират директно:

2. Изчисляване на определен интеграл (Таблица 2):

.

- интегриране по части, а след това, вместо да доведе до константи за интеграция замени несигурни граници на интеграция през основните теорема формулата:

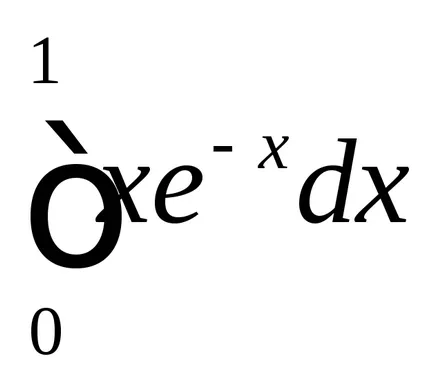
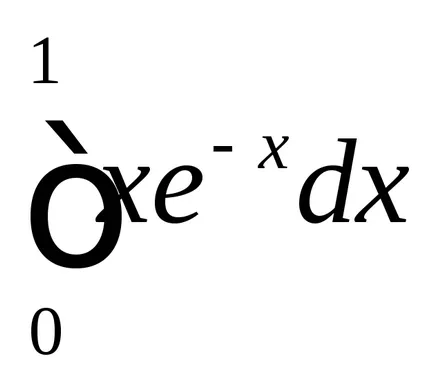
3. Изчислява областта на фигурата, ограничена от линии (Таблица. 3).

.

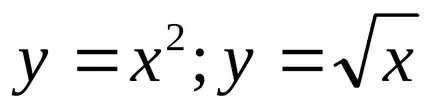
Тези линии означават извит участък, площта на които може да се намери като разликата в площта под функцията

и функция.

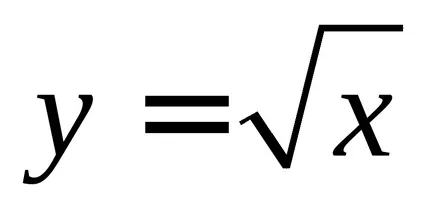
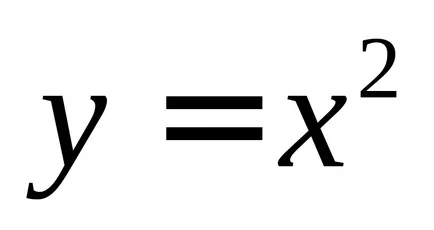
1. В партидата на членове п N продукти имат латентна дефект (Таблица 1). Каква е вероятността, че произволно взет от к продукти продукт м са дефектни?

Вероятност латентна дефект в произволно избран равни части р = N / N = 5/20 = 0,25. Изборът на произволен брой продукти могат да бъдат представени като последователен повторение без проба, която е обект на Бернули след изпитания. Следователно, вероятността от дефектни продукти тегли 2 при избора на продукти 4 произволно от общата проба е:

2. магазина изложени за продажба п продукти, включително нестандартни продукти к (Таблица 2). Каква е вероятността, че произволно взети м продукти са с ниско качество?

Вероятността, че продуктът ще бъдат взети случайно нередовни е р = к / п = 6/16 = 3/8.

Всеки тест (проба продукт) независимо от другите, така че вероятността от случайно вземат две последователни лошо качество на продуктите е продукт на вероятностите: P (2) = 3/8 ∙ 3/8 = 9/64 = 0,140625.

3. В завода за сглобяване на същите компоненти тип, получени от три растения в количество от: n1 с първото растение, N2 с второто растение, n3 в на третия (Таблица 3.). Вероятност за производство на качествени продукти на земята по време на второто растение P1 P2. третата p3. Каква е вероятността, че продуктът е взето на случаен принцип ще означава за мен?

По формулата на общата вероятност, вероятността от възникване на събитие в искането пред него друг предварително събитие е сумата от продукти от различни събития, водещи до възможността за поява, събитията, които се интересуват от вероятността за настъпване на това събитие да се предшестват ако събитието вече се е случило:

4. Предвид дискретни разпределение на случайната променлива X (Таблица 4). Намерете средната стойност и стандартното отклонение.

Математическият очакването се определя като

Дисперсията на известно очакваната стойност се определя като

Стандартното отклонение е корен квадратен от дисперсията:

5. В града има N дистрибуторски центрове (раздел. 5). Вероятността, че желаната позиция клас не е в тези бази данни е същата и равно на стр. Бъдете разпределение право на броя на базите в който желания продукт не е наличен в момента.

Разпределение на броя на базите в който желания продукт не е наличен в момента с еднаква вероятност за липса на стоки от всяка от базите се подчинява на вероятностно разпределение на Бернули проучвания:

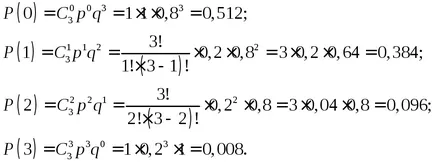
По този начин разпределението на броя на основи, при което желаната позиция понастоящем не се определя по следната таблица:

Броят на основи, при което желаният продукт не е на разположение в момента

6. непрекъсната случайна променлива има нормално разпределение. Нейният очакване е равно на Mx. стандартно отклонение

(Табл. 6). Намерете вероятността, че резултатът от теста за случайна променлива ще поеме стойност в диапазона от (а. Б).

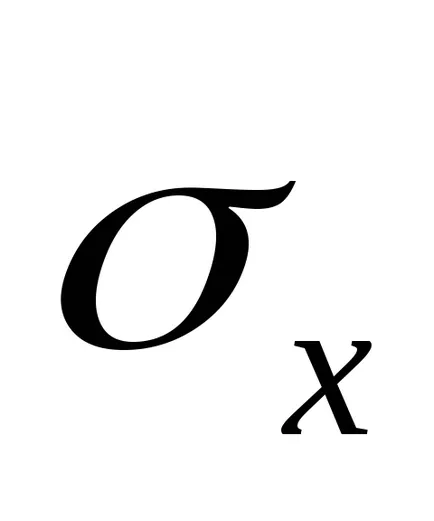
Ml = 14;

= 3; а = 10; б = 15.

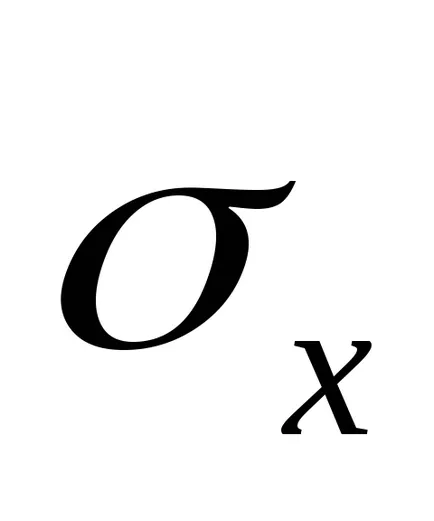
Вероятността да бъде във всеки интервал за непрекъснато разпределени количества равни на:

Използвани собственост Odd Лаплас функции и стандартни таблици на функцията на Лаплас.

1. Изчислете и относителната честота хистограма за групираните данни (Таблица 1) Когато мл - влизат в вариант честота празнина. (XI; XI + 1).

Безпристрастен вариацията проба и (х) се определя въз основа на изчисление на извънматочна (емпирично) дисперсия D (х). За да се изчисли общата сума определи първата честота: 31 + 14 + 28 + 27 = 100.

Математическият очакването се определя като

Дисперсията на известно очакваната стойност се определя като

Тогава безпристрастен вариация:

3. Проверка на нулевата хипотеза, че предварително определената стойност A0 е математически очакването на случайна променлива нормално разпределени на ниво значимост от 5% за дуплекс критичен регион, ако в резултат на обработката на п = 10 проби, получени от пробата означава обем

, и проба стандартно отклонение ravnos1 (Таблица 3).

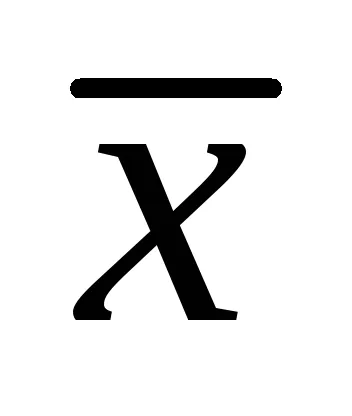
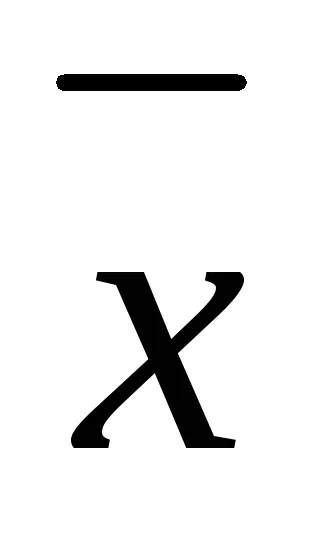
Ние изчисли дисперсията на всяка проба в отделна, предварително изчисляване на математически очакването, и след това сравнение на дисперсията чрез разделяне на по-голямата от тях по-малки:

Очакванията на х се определя като

Дисперсия X по известен очакваната стойност се определя като

Очакванията на у е дефиниран като

Дисперсията на известно очакваната стойност се определя като

Разделете голяма дисперсия и по-малък получаване F = 50,0622 / 15,7156 = 3186, и сравняват резултатите, получени от критерий на Fisher на половината ниво на значимост а броят на степените на свобода, по-малък единица - Ftabl = 2.48 - Фишер-Снедекор маси 0.05 ниво на значимост и 14 степени на свобода за всяка променлива. По този начин, като стойност е по-малка в сравнение с отчитането на критерий, основната хипотеза за равенство на отклонения се отхвърля (не е приемливо), но трябва да се приеме алтернативна хипотеза върху неравенството дисперсии на две проби от данни.

5. Виж селективен линейна регресия уравнение Y да X въз основа на таблицата на съответствието (Таблица 5).

Ние изчисляваме следните суми:

Ние изчисляваме средната стойност и дисперсията на всяка променлива:

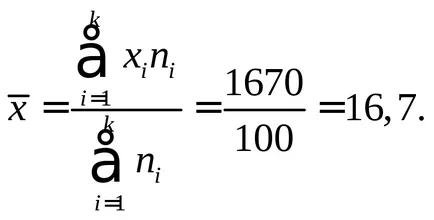
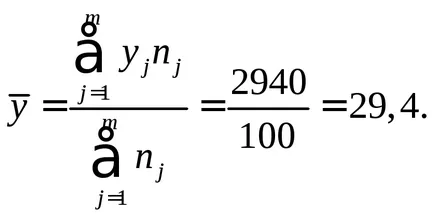
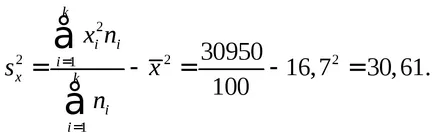
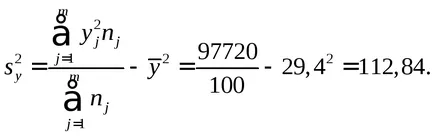
Изчисляваме параметър μ:

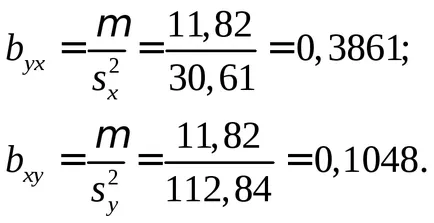
Сега можете да получите на регресия уравнение на Y на X и X на Y в най-чистата му форма:

Ние изчисляваме необходимите коефициенти на уравнението: