Логическите операции на предикати - studopediya

За предикат Р (х): "х - четен брой" и Q (х): «х кратно на 3» връзка Р (х) LQ (х)

Определение. Дизюнкция на две предикат Р (х) и Q (х) се нарича нов предикат Р (х) V Q (х), която е на стойност "фалшива" в тези и само тези стойности х-niyah Î M, в която всеки предикат оценява с "фалшив" и отнема стойност "истина" във всички останали случаи.

Домейн на валидност на предикат Р (х) V Q (х) е обединението на домени истина предикат Р (х) и Q (х), т.е.. IPVQ = Ip È Интелигентност.

Пример: За предикат Р (х) и Q (х) истинската обхвата на тяхната дизюнкция е обединението на техните полета на истината:

Определение. Отрицание предикат P (х) се нарича-ОЗНАЧАВА нов предикат, който е на стойност зададена "истинска" за всички стойности на х Î М в която Р (х) е предикат оценява с "фалшиви", и приема стойността "фалшива" за стойностите на х Î М приема стойността "истинска". В кото-ryh предикат Р (х)

От тази дефиниция следва, че графиката:

Пример: образуване на предиката. "X - нечетно число," Неговата истина домейн:

Тъй като за всеки фиксиран х Î М-Spra равностойност са валидни

Графика: област отговаря на истината на сенчеста част:

Помислете за няколко примера за намиране области на предиката е вярно.

1. В комплект M = предикати посочени:

А (х) "не се дели NA5 х" (х) "просто число х" (х). "Умножение х 3» Намерете много истина предикат:

Намираме предикатното поле валидност А (х) В (х) и - "х не е кратно на 3 ':

Предикатът замени косвено.

Предикатна съответства на формулата, определена алгебра:

2.Izobrazit Ойлер диаграма - Вен област истина предикат: а)

На първо място, ние извършваме реализация, като се има предвид предикат да казва:

Предикатна отговаря на истината домейн, определен от формула комплекти алгебра:

Диаграма е както следва:

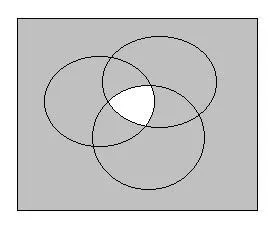
ОБЛАСТ истина предикат е оцветен в сиво.

Предикатна отговаря на истината домейн, определен от формула комплекти алгебра:

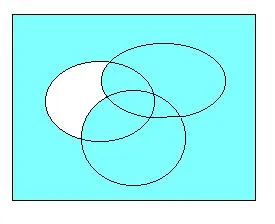
ОБЛАСТ истина предикат оцветен.

3. Запишете предикат Получената логически операции на предикати Р (х), Q (х), R (х), истина площ сенчести които: