Linear неразделна и циркулация на полето на вектор

Определяне на линейна интегрална

Да предположим, че в $ пространствената област \ mathbf> $ е непрекъсната вектор поле $ \ бар (\ mathbf>), \ mathbf> $ - гладка крива лежи в $ \ mathbf> $. интеграл линията на полето $ \ бар $ по линия $ \ mathbf> $ се нарича линия неразделна по дължината на дъгата на вътрешния продукт $ \ бар (\ mathbf>) $ на вектор $ лентата \ единица тангента (\ mathbf>): W = \ вътр \ limits_L (М) \, DS> $.

Тъй като потокът на тази интегрална може да бъде представен по различни начини. Така че, като се има предвид, че продуктът от $ \ бар (М) $ в DS $ $ дава промяната на радиус вектора на точка $ \ mathbf> $, т.е. $ \ Бар \ cdot DS = г \ бар = DX \ бар + ди \ бар + DZ \ бар $, след $ W = \ Int \ limits_L> $ и $ W = \ Int \ limits_L $. Следователно, линията неразделна, и може да се изрази чрез линейна неразделна координатите.

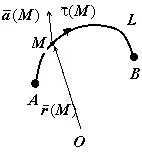
Физическият смисъл на линейна интегрална.

ако $ \ бар (\ mathbf>) $ - силово поле, $ W $ е областта в този момент се движат на материала по линия $ \ mathbf> $ видите тройни интеграли ..

Основните свойства на линеен неразделна.

$ \ Int \ граници _ \, DS> = \ Int \ граници _ \, DS> + \ Int \ граници _ \, DS> $. Посока на всяка от частите на $ \ mathbf> _ $ и $ \ mathbf> _ $ трябва да бъде същата като на цялата крива $ L_1 \ чаша L_2 $,

3). Когато посоката по $ \ mathbf> $ линейни интегрални промени подписват.

Това е следствие от факта, че вектор $ лентата \ (\ mathbf>) $ се променя на - $ \ бар (\ mathbf>) $.

4). Ако $ \ mathbf> $ - вектор поле линия и се движи в посока на областта, а след това $ \ mathbf >> 0 $. В този случай, вектор $ \ лента (\ mathbf>) $ колинеарни $ \ бар (\ mathbf>) $, така че $ \ бар \ cdot \ бар = \ mathop \ бар> \ limits_> = \ лаборатория \ бар \ лаборатория> 0 $.

Изчисление на линия неразделна

Като всяка линия неразделна, линия неразделна се изчислява чрез редукция на определен интеграл на параметър крива обикновено изчислява линия неразделна $ W = \ Int \ limits_L $. Ако кривата с параметричен спецификация е на форма $ L: \ ляво \ \ Точно така. t_0 \ leqslant т \ leqslant t_k $, където $ х (т), \, у (т), \, Z (т) $ - непрекъснато диференцируема функция, след $ W = \ Int \ limits_L = \\ = \ Int \ ограничения _ ^ "(т) + Q (х (т), Y (т), Z (т)) \ cdot" (т) + R (х (т), Y (т), Z (т)) \ cdot "(т)> \ полето] DT> $.

интегриране на посоката на движение се определя от посоката на кривата.

поле вектор Circulation

Тираж се нарича линия интеграл от областта на вектор на затворена крива $ \ mathbf> $: U $ = \ Съвместният \ limits_C> $.

Обикновено се казва, че движението е характерно за въртене капацитета на терена. Това се отнася до следното. Ако вектор силови линии са затворени, а след това, както вече видяхме, циркулацията на това в посока на областта е положителен, докато в хидродинамичен тълкуването на частици предене течност към тези затворени линии. Да предположим сега, че сегашните линии са произволни, представете си, в размер на $ \ mathbf> $ затворен контур $ \ mathbf> $. Ако в резултат на движение на флуиди, тази верига ще се завърти областта има въртене на капацитет, абсолютната стойност на движението ще определи ъгловата скорост U $ \ рампа $, толкова по-висока скорост>, циркулация марка ще покаже дали посоката на въртене съвпада с посоката на интеграция.

Вижте също:

Механична прилагане на двоен интеграл

Изчисляването на повърхността интеграл от първи вид

Свойства на двойни интеграли

Формула. функции между половете и за еквивалентност на формули. Ключови равностойност

Напред към съдържанието на $ \ стрелкаНадясно \ стрелкаНадясно \ стрелкаНадясно $