Личен сайт - функция у грях х, у COS х, у MF (х), у е (KX), у TG х, у CTG х
След това образуват графика. Получаване на половин вълна, най-високата точка от които (π / 2; 1). Тази графика на функция у = грях х в интервала [0; π]. Към диаграми симетричен полувълнов (симетрична около произход, т.е. на интервал-я). Това полувълнов гребен - на оста х с координатите (1, 1). Резултатът е вълна. Тази графика на функция у = грях х в интервала [-π; π].
Можете да продължите вълна благодарение на конструкцията и на интервала [π; 3π], [π; 5π], [π; 7π] и т.н. Във всички тези сегменти графика на функцията ще изглежда по същия начин, както в интервала [-π; π]. Снабдете се с непрекъсната вълнообразна линия имат същите вълни.
Графика на функция е синусоида (понякога го наричат косинус).
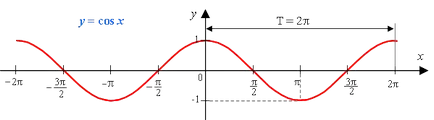
1) областта на функцията - набор от реални числа.
2) Област на стойности на функцията - интервала [1; 1]
3) Това е дори функция.
4) Това е непрекъсната функция.
5) Координатите на пресечните точки на графиката:
- с абсцисата: (π / 2 + πn 0),
- с оста ордината: (0; 1).
6) В интервала [0; π] функция намалява интервала [П; 2π] - се увеличава.
7) В интервалите [-π / 2 + 2πn; π / 2 + 2πn] функция се положителни стойности.
На интервали [π / 2 + 2πn; 3π / 2 + 2πn] функция се отрицателна стойност.
8) пропуски увеличават: [-π + 2πn; 2πn].
Низходящо интервали: [2πn; π + 2πn];
9) минимална точка: π + 2πn.
функция на максималната точка: 2πn.
10) Тази функция е ограничена по-горе и по-долу. Най-малката стойност функция -1,
1, най-голямата стойност.
11) Това е периодична функция с период на 2π (Т = 2π)
Вземете предишната функция Y = защото х. Както вече знаете, нейната графика е синусоида. Ако умножава косинус функция на определен брой т, след вълната ще се простира от оста х (или свиване, в зависимост от стойността на m).
Тази нова вълна и ще графиката на у = MF (х), където m - произволно реално число.
Така функция Y = MF (х) - е познат ни функция у = е (х), умножена по т.
Извършване на разтягане или компресия, трябва първо да се изгради само един полу-вълна синусоида, а след това завърши целият график.
Ако функция у = МФ (х) води до разтягане на синусоида оста х или х-оста на компресия. функция у = F (KX) води до разтягане на у-ос или у компресия ос.
И к - всяко реално число.
График на тази функция, трябва първо да се построи половин вълна синусоида, а след това завърши на целия график.
Графиката на функция у = TG х е tangensoida.
Достатъчно е да се изгради графиката в интервала от 0 до П / 2, след това може да продължи симетрично в интервала от 0 до 3π / 2.
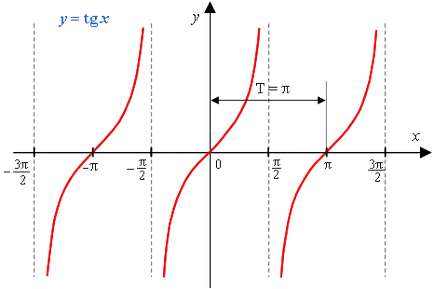
1) областта на функцията - множеството на всички реални числа, с изключение на номерата на формата
х = π / 2 + πk, където к - е всяко цяло число.
Това означава, че функцията на графика не е точката за принадлежност към права линия х = π / 2,
с права или х = 3π / 2, или директно х = 5π / 2, или директно х = -π / 2, и т.н.
2) стойности Площ функция (-∞ + ∞)
3) Това е нечетно функция.
4) е непрекъсната функция в интервала (-π / 2; π / 2).
5) Това е периодична функция с основен период π (Т = π)
6) се увеличава в интервала (-π / 2; π / 2).
7) Тази функция не се ограничава до горната или долната част. Той има нито най-малкото, нито най-големите ценности.
Графиката на функция у = CTG х е tangensoida (понякога се нарича kotangensoidoy).
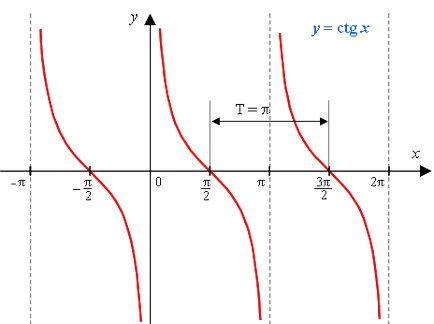
1) областта на функцията - множеството на всички реални числа, с изключение на номерата на формата
х = πk, където к - всяко цяло число.
2) стойности Площ функция (-∞ + ∞)
3) Това е нечетно функция.
4) Това е непрекъсната функция.
5) Това е периодична функция с основен период π (Т = π)
6) функция намалява в междината (πk; π + πk), където к - е всяко цяло число.
7) Тази функция не се ограничава до горната или долната част. Той има нито най-малкото, нито най-големите ценности.