Личен сайт - дори и нечетни функции
Дори и нечетни функции. периодични функции
Дори е функция, чийто знак не се променя, когато х марка.
С други думи, за всяка стойност на х, F на равенство (-x) = F (х). X знак не влияе знака на ш.
Насрочете дори функция симетричен по отношение на осите (Фиг.1).
Примери на дори функции:
Обяснение:
Да разгледаме у функция = х 2 или у = Х2.
За всяка стойност на х е положителен функция. X знак не влияе знака на ш. Графиката е симетрична по отношение на координатните оси. Това е още по-функция.
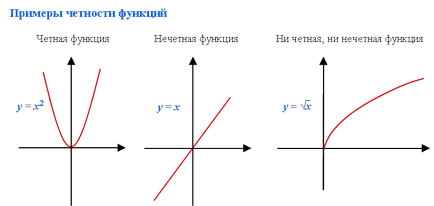
Странно е функция, чийто знак варира в зависимост от х марката.
С други думи, за всяка стойност на х, равенството е (Х) = -f (х).
Графика нечетен функция симетричен относно произхода (Фигура 2).
Примери нечетен функция:
Обърнете функция у = -x 3.
Всички стойности са в нея ще бъде отрицателен. Това е знака на х влияе знака на ш. Ако независима променлива - положително число, и положителен функция ако независимата променлива - с отрицателна стойност, тогава отрицателен функция: F (-x) = -f (х).
График функция симетрична спрямо. Това е странно функция.
Свойствата на четна и нечетна функция:
1) Размер на дори функции е дори функция.
Сумата от нечетен функция е нечетно функция.
2) Ако функция F е още, тогава функция 1 / F дори.
Ако е е нечетен, тогава функция 1 / F е нечетен.
3) Продуктът от две функции дори е още функция.
Продуктът се от две нечетни функции е още по функция, също.
4) Продуктът на дори и нечетен функция е нечетно функция.
5) производно на още функция е нечетен и нечетните - дори.
Не всички функции са още или странни. Има функции, които не са предмет на такава градация. Например, в основата на функция у = √h не принадлежи към нито дори странно функция (Фигура 3). При изброяването на характеристиките на тези функции трябва да се обърне адекватно описание на: всеки дори, или странно.
Както знаете, на честотата - е повторяемостта на някои процеси с определен интервал. Функции, описващи тези процеси се наричат периодични функции. Това означава, че функционира чиито графики са елементи, повтарящи с някои числени интервали.