Квадратна матрица

Четвърти ред квадратна матрица. АП елементи образуват основната диагонална квадратна матрица. Например, основният диагонал на матрица 4x4 на фигурата съдържа елементи a11 = 9, А22 = 11, А33 = 4, А44 = 10.

В математиката, квадратна матрица - матрица. в които броят на редовете е равен на броя на колоните, и този брой се нарича ред на матрицата. Всеки две квадратни матрици на същия ред, могат да се добавят и умножени.

Квадратни матрици са често използвани да представляват прости линейни съответствия - като щам [ен] или въртене. Например, ако R - квадратна матрица, представляваща въртене (ротация матрицата) и V - вектор колона. определяне на положението на точка в пространството, продуктът на Rv осигурява друг вектор, който определя положението на точката след завъртането. Ако V - ред вектор. същото превръщане може да се получи използвайки където VR Т. R T - R транспониране матрица.

Диагонални матрици и триъгълни

Ако всички елементи извън главния диагонал са равни на нула, A се нарича диагонал. Ако всички елементи по-горе (по-долу) на главния диагонал са нула, А е наречен по-ниска (горен) триъгълна матрица. Триъгълна матрица, чиито елементи са диагонал всички равно на 1, наречен unitriangular [2] [3].

идентичност матрица

идентичност матрица En размер п - е N х N матрица, в която всички елементи на главния диагонал са равни на 1, и други елементи са равни на 0 (често се използва вместо буквата буквата Е I [4]) [1]. По този начин,

идентичност матрица размножаването на матрица на оставя непроменена:

Симетрична и antisymmetric матрица

Квадратна матрица A. съвпада с транспониране. т.е. A = A Т. нарича симетрична. Ако А е различен от знака на транспонирана матрица, т.е. А = -А Т. След това се нарича antisymmetric (или antisymmetric) [4] [5]. В случай на сложни матрици на концепцията за симетрия често се заменя с понятието за самостоятелно долепени. матрица удовлетворява уравнението A * = А. наречен Hermitian (или selfadjoint); Тук звездичка означава Hermitian операция спрежение. където значението на - заместване на всеки елемент в оригиналната матрица комплекс спрегнатата транспозиция последвано брой на получената матрица [6] [7].

Според спектрален теоремата за реални симетрични матрици и сложни Hermitian матрици има база, състояща се от собствени вектори; по този начин, всеки вектор пространство може да бъде представена като линейна комбинация от собствени вектори. И в двата случая, всички собствени стойности са реални. [8] Тази теорема може да бъде удължен до случая на безкраен, когато матриците имат безкраен брой редове и колони.

Инверсия на матрици

Квадратна матрица А се нарича обратимо или неособена матрица. ако има матрица Б. така, че

Ако съществува матрица В, е уникален и се нарича обратна на А и записва като -1.

определена матрица

Точките отговарят на уравнение Q (х, у) = 1
(Елипса).

Точките отговарят на уравнение Q (х, у) = 1
(Хипербола).

Симетрична п х п матрица се нарича положителен определен (съответно отрицателно или определен неопределен), ако за всички ненулеви вектори х ∈ Rn съответстващ квадратна форма

Това отнема само положителни стойности (съответно отрицателни стойности, или и двете, и други). Ако квадратна форма отнема само неотрицателна (или само не-положителна) стойност, симетричен матрица се нарича положителен semidefinite (съответно отрицателно semidefinite). Матрицата ще бъде несигурен, ако тя не е нито положителна, нито отрицателна semidefinite. [11]

Симетрична матрица е положително определена единствено и само ако всички свои собствени стойности са положителни [12]. В таблицата в дясно показва две възможни случаи за с размери 2 х 2 матрици.

Ако използвате две различни вектори, ние се получи форма билинеарно. свързана с:

ортогонална

Ортогонално матрица - квадратна матрица с реални елементи, чиито редове и колони са ортогонални единичен вектор (т.е. ортонормирани). Човек може да се определи ортогонална матрица като матрица обратен е равна на транспозиция на [7]:

Един ортогонална матрица А е винаги обратимо (-1 = A T А), е единно (А -1 = A *) и нормален (A * А = AA *). В детерминанта на всяко ортогонална матрица е равна или на един или -1 [14]. Умножаването от ортогонална матрица определя линейна трансформация аритметика пространство R п ^>. която в случая на матрица с фактор 1 е едно завъртане. и в случай на матрица с детерминанта -1 е просто отражение. или суперпозиция на отражения и въртене.

След квадратна матрица А (TR (А)) е сумата от елементи на основната диагонала. Докато умножение на матрици, най-общо казано, не комутативен, следа от произведение на две матрици не зависи от реда на факторите:

Това следва директно от определението на продукта за матрица:

Също така трябва да бъде транспонирана матрица е равна на пистата, за да го, това е,

определящ

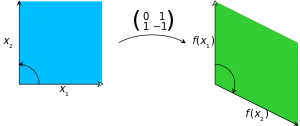
Линейната картографиране на някои R 2. намалената матрица. В детерминанта на матрица е 1, и въпреки зелени площи успоредник остава 1 показва промяна на ориентацията. От вектора са движение на часовниковата стрелка, както и техните образи са в обратен ред.

Det на детерминанта (A) или | A | квадратна матрица A - е число определяне на някои свойства на матрицата. Матрицата е обратим, ако и само ако. когато нейната детерминанта е различна от нула. Абсолютната стойност на детерминанта е равна на площта (R2) или обем (в R3) на изображение единица квадрат (или куб), а знакът на детерминанта съответства на ориентацията на съответния дисплей - детерминантата е положителен, ако и само ако ориентацията се поддържа.

Детерминанта 2 х 2 матрица се изчислява по формулата

Детерминанта 3 х 3 матрица използва 6 броя (член на sarrus). Дълъг Лайбниц формула [ен] обобщава тези две формули за всички измерение [15].

В детерминанта на продукт на матрици е продукт на детерминанти фактори:

Добавянето на всеки ред с коефициента за друга линия, или с всяка колона на друг коефициент колона не променя детерминанта. Прехвърляне на два реда или колони определящ води до промяна в знака на [17]. Използването на тези операции, всяка матрица може да бъде намален до по-ниска (или горната) триъгълна матрица, и за такива матрици детерминанта е равна на произведението от основните диагоналните елементи, което дава метод за изчисляване на фактор на всяка матрица. И накрая, Лаплас теорема изразява определящ фактор по отношение на малолетни и непълнолетни лица. т.е. детерминанти на малки матрици [18]. Тази теорема позволява рекурсивни изчислителни детерминанти (започвайки с детерминантата на матрицата 1 х 1, или дори с матрица детерминанта 0 х 0, което е равно на 1), който може да се разглежда като еквивалент Лайбниц формула. Детектори могат да бъдат използвани за решаване на линейни системи, използващи метод Cramer на [19].

Собствени стойности и собствени

ДълЖината на брой и по-различна от нула вектор ст. на задоволяване на уравнението

наречен собствена стойност и собствен вектор на А, съответно [20]. Броят е собствена стойност λ п х п матрица А, ако и само ако А -λE не обратно, еквивалент

От неизвестен полином PA [ен] X. получи детерминанта Det (XE -А), наречен характеристика полином на матрица А. Това нормализирана полином [ен] * степен п. Така, PA уравнение (λ) = 0 има максимален на п различни решения, т.е. собствени стойности [21]. Тези стойности могат да бъдат сложни, дори и ако всички елементи на матрицата са истински. Според теоремата на Хамилтън - Cayley. рА (A) = 0. т.е. чрез заместване на самата матрица в характерната полином получи нула матрица [22].