Кривите, посочени в полярни координати,

Сложете точка на часовниците втора употреба и ще се смесват с точка по протежение на втората страна с постоянна скорост, без да се обръща внимание на еднаквото движението на часовника в кръг. Тогава точката ще опише крива, наречена архимедова спирала. Изобретението на тази крива се дължи на Конон Самос, въпреки че основните му свойства са описани Архимед (с. 287-212 пр.). Архимед, по-специално, е известно, че разстоянието между две последователни навивки на спиралата е постоянна и равна на 2π (фиг. 3).

Между другото, тъй като на тази функция в подреждането се оказва истински образ на спиралата на Архимед може да се види, например, гледане на здраво увити ролка хартия с неговата крайна повърхност.

На извънкласни дейности е полезно да се покаже на строителството на първия завой на спиралата на Архимед.

Начертайте кръг. И раздели своята радиус OA в п равни части.

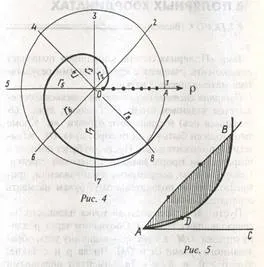
Нека п = 8. равенство всички точки, разделящи гредите от центъра О на кръга и им брой (фиг. 4). 1 заедно точка на линията бележка на разстояние

OA от центъра на кръга. 2 по линията на базовата точка на разстояние

ОА на линията 3 - точка на разстояние

ОА и т.н. 8 по линията ще се постави точка на разстояние

Постоянно гладка крива, свързваща точките с данни, ще видим първия завой на спиралата на Архимед. Конструкцията ще бъде още по-точно, толкова повече точки, разделящи радиуса и обиколката е избран първоначално.

Архимед спирала се използва като линия позволява предварително определен ъгъл да се разделят произволен брой равни части. Някои от рисуване в старата част на работните инструменти, включени метална плоча с гравиран върху него внимателно спирала от Архимед. С помощта на това устройство е било лесно да се разделят на ъгъл на две равни части. Например, за ъгъл trisection BAC го приложи част достатъчно плоска плоча една от ъгъла на рентгенови лъчи (фиг. 5) и да се раздели полученият сегмент AB в 3 еднакви порции. Arc спирала трябва да се направи с една степен радиус AO = - AB. Тогава ъгъл CAO ще бъде равен на една трета от БКК на ъгъл.

В областта на Архимед спирала то намира приложение в така наречената люлка-камера Меча които преобразуват въртеливо движение в линейно движение шайби прът. В някои условия (например в час), необходими за преместване на пръта равномерно. Уверете се, това е възможно, очертаване на профила на зъбните колела в спирала на Архимед.

Като втори обект за използване архимедова спирала в областта може да предизвика самостоятелно центриране на патронника (фиг. 6), което направляващите канали, оформени в една спирала на Архимед. С едно завъртане на диска патронник челюсти движат върху радиално разстояние стойност съседни канали.

В допълнение, с формата на Архимед спирала да има звук, записите и една от частите на шевна машина - механизъм за равномерно навиване на конеца на калерчето.

→ + ∞ може да се види, че

→ + ∞ и спирала разгъване обратно на часовниковата стрелка (фиг. 7)

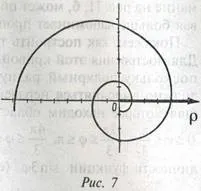
Той описва логаритмична спирала точка преместване по втора посока не е с постоянна скорост (в случая на архимедова спирала), и с увеличаване, и това увеличение пропорционално на разстоянието от центъра часа.

Логаритмична спирала може да се строи с помощта на така наречената златна правоъгълника, т.е. тази, в която съотношението на страните е равно на златното съотношение:

Ако AVSDotrezat площад злато правоъгълник със страна, равна на по-малката страна на правоъгълника, а след това отново да получи златен правоъгълник EFSD, но по-малък. Ако продължим този процес по-нататък, а след това се свържете на върха на плавна крива на площади, както се прави на фиг. 8, ние получаваме на логаритмична спирала.

Логаритмична спирала има редица интересни свойства:

• разстоянието между последователните навивки образуват геометрична прогресия;

• последователността на дължините на радиусите, които са равни ъгли помежду си, също представлява геометрична прогресия;

• формира в процеса на разширяване на сектори, като прихваща радиуси подобен drugdruga.

На логаритмична спирала често се срещат в природата и е свързано с някои видове растеж. Толкова много Миди последователни намотки не са идентични, както и все по-често се сгъсти. В много случаи приблизителните дебелината на последователни завои образуват геометрична прогресия. Докато мидена черупка самата не може да се счита за живеене, то се формира от отглеждане на организма. Един от най-простите начини за изграждане на новото вещество автоматично води до образуването на форма в непосредствена близост до логаритмична спирала. В много черупки поразително близък се намери съответствие между резултатите от измерванията и теоретичните стойности очаква за точно логаритмична спирала (фиг. 9). Слънчогледовите семена са разположени на дъги от характерен близо показват съответните измервания към логаритмична спирала дъги. Поради тези факти, някои учени смятат, логаритмична спирала крива, която е един от изразите органични законите на растеж.

Прилагане на логаритмична спирала в областта въз основа на свойството, че всички напречни радиус крива вектори под същия ъгъл 2. След това свойство базирано приложение на логаритмична спирала в областта. По този начин, въртящи се лопатки в различни машини (фиг. 10) имат профил профилирана дъга спирала, при което ъгълът на рязане (ъгъла между режещото острие и посоката на скоростта на въртене) остава постоянна по подвижния нож ръб, която осигурява по-малко износване.

Тръбна сумиране струя вода до водноелектрически остриета турбинни колела, има профил нарязан в дъга на логаритмична спирала. Това гарантира минимална загуба на енергия за промяна на посоката на потока, и следователно, налягането на водата се използва с максимална ефективност.

В историята на математиката логаритмична спирала се споменава за първи път през 1638 от Декарт, който дефинира нова спирала като линия, в които съотношението на дължината на дъгата до съответния радиус вектор е постоянна.

Най-логаритмична спирала - крива с "твърд" характер. Това не променя своя характер в много трансформации, които са чувствителни към други криви. Компресиране или декомпресиране на спиралата около полюсите - същите, които го превръщат в определен ъгъл. Този имот е логаритмична спирала е бил открит от Якоб Бернули нарича го spiramirablis- прекрасен спирала. Отворете свойствата на логаритмична спирала Бернули остават непроменени в различни реализации, така впечатлен ученият, че той е склонен да им даде едно мистично значение. Якоб Бернули завещал да извая логаритмична спирала върху надгробната му плоча, придружен от изображение «Eademmutateresurgo» латинска фраза - "Промени и съживява старите."

На следващо място, нека разгледаме няколко примера за криви, полярни уравнения, които съдържат тригонометрични функции. Изграждането на тези криви може да се направи на точките, в които

Тя заема стойности от 0 до 2π.

Семейството на рози Grande

където к - положителна константа.

В XVIII век. Италианската геометрик Гуидо Grandi (1671-1742) е създаден роза. Не, не и тези красиви Най цветя, които най-вероятно мислят. Rosa Grande ни зарадва с правилни и плавни линии, но очертанията им не са изрод на природата - те са предварително определени от специално подбрани математически отношения. Тези криви бяха предизвикани от природата, защото в повечето случаи на листа или очертанията на едно цвете е крива симетричен около оста.

Семейството на рози Grande има имот, който се намира в природата и не веднага забеляза: тъй като

цялата крива се намира във вътрешността на кръга. С оглед на периодичността на тригонометрични функции розови листа се състои от идентични, симетрични по отношение на най-голямата радиуси, всеки от които е равна на 1.

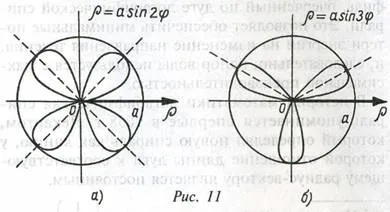
Най-добро "цветя" са получени за к = 2 (chetyrehlepestkovaya роза), и за к = 3 (трикратно роза, въпреки че на читателя да се отбележи, на фиг. 11 Ь, може да изглежда, че тази крива е по-скоро като перка).

Ще покажем как да се изгради trohlepestkovuyu роза. първата бележка, за да се изгради тази крива, тъй като радиуса на полярен или отрицателен, а след това неравенство трябва да бъдат изпълнени Sin3

≥0, да решат кой е площта на допустимите ъгли: 0≤

Поради Sin3 функция периодичност

(Неговият срок е равен на

) Е достатъчен, за да се конструира крива на ъгли

, и останалите две интервали използват честота. Така pust0≤

варира от 0 до 1. Sin3

Тя варира от 0 до 1, и следователно,

варира от 0 до 1. Ако ъгълът се променя от

, промените в радиус от 1 до 0. Така заболяване, когато ъгълът

, tochkana самолет описва крива, подобна на формата на венчелистче и се връща към произхода. Същата бе получен когато ъгълът

Той варира между

. Сега помислете как да се построи крива, дадена в полярни координати с уравнението

- периодично с период π, освен това,

така че това е достатъчно, за да се построи крива през първото тримесечие, а след това я обърнете по отношение на оста у и честотата на използването му за създаването на кривата в третото и четвъртото тримесечие.

monotonnovozrastaet от 0 до 1 и [

;

] Намалява монотонно от 1 до 0. По този начин, ние получихме една роза венчелистче, който се намира в първото тримесечие. Останалите три листенца, получени ако извивката в останалите тримесечия.

Трябва да отбележим следните интересни свойства chetyrehlepestkovoy рози:

• chetyrehlepestkovaya роза е траекторията на перпендикулярите падна от произхода на дължината на сегмент 1, краищата на която се плъзга по координатните оси;

• площта под chetyrehlepestkovoy роза, е

Grundy Roses са били приложени в практиката, по-специално, ако една точка по линия, колебае се върти с постоянна скорост около фиксирана точка - центъра на трептене, траекторията на този етап ще се повиши.

По принцип, ако к - цяло число, то се състои от една роза 2klepestkov за още по-к и от к: за к странни листенца. Ако к - рационално число (к =

, венчелистчетата розови състои от М в случая, когато и двете от m и п нечетен и листенца от 2 m, когато един от тези номера е дори; където стъпката частично се припокриват. Ако к - ирационално число, розата се състои от безкраен брой припокриващи венчелистчета.

Лемниската на Бернули - един от най-забележителните алгебрични линии. От формата на кривата следва уравнението, кривата се състои от две симетрични листа (на външен вид, тази крива наподобява обърнат осем или лък). За точки лемниската неравенство трябва да притежава-равенство sos2

, обаче се намира между редовете Y = ± х. Имайте предвид също така, че

Ще покажем как да се изгради лемниската на Бернули. Но първо, ние се отбележи, че както квадрата на полярния радиус не е отрицателен, трябва да се извършва sos2 неравенство

. Решаването на този неравенство, ние откриваме, че границите на допустимите ъгли:

Поради sos2 функция периодичност

(Период му е равно на π) е достатъчен, за да се изгради графика за ъгли

и в други случаи, честотата на употреба