Консервативните и не-консервативните сили

Всички сили, възникнали в механиката на макроскопичните тела се разделят на консервативни и не-консервативни. Наречен консервативни сили, чиято работа не зависи от формата на пътя между две точки (когато се движат между тялото).

Един пример е консервативните сили, като тежестта. Изчислява работата на тази сила в точката на преминаване на материала от позиция 1 до позиция 2 заедно R12 линия сегмент:

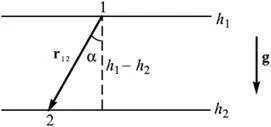
Фигура 4.3 - Определяне на работната сила на тежестта

където h1 и h2 - височина, на която материалната точка в началото и в края на пътя. Те се оценяват от всякакви своеволни ниво, например от почвата или от морското равнище.

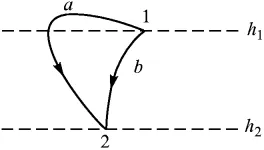
Формулата за наляво и надясно, докато се движи по произволна крива 1А2 или 1B2 (фигура 0.3).

За да докаже това, ние трябва да се раздели по целия път от хоризонтални равнини на малки секции, всяка от които може да бъдат взети като права линия. Прилагането на всеки раздел от получена формулата и добавяне на полученото произведение, стигаме до предишния резултат. По този начин, на действието на гравитацията не зависи от формата на път. Тя се определя само от началната и крайната позиция на движещата се точка.

В допълнение, като се сравняват

Ние стигаме до извода, че

това е, когато се движат в гравитационното поле на стойността

Тя е, както знаете, се нарича общата енергия на системата и на сумата от кинетичната и потенциална енергия. В рамките на потенциалната енергия е необходимо да се разбере стойността тук.

Втори пример за консервативните сили на така наречените централни сили.

Пример за такава сила, може да послужи като сила на гравитационно привличане на Земята до Слънцето (или на Луната до Земята) ..

Ние показваме, че работата на централната сила зависи от формата на пътя се определя само от началните и крайните позиции на точката на материал (фигура 4.4). За да направите това, ние извършваме безкрайно изместване.

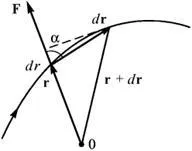
Фигура 4.4 - От определението на централните сили

при което - нарастване на разстоянието до центъра (фигура 4.4). По този начин,

Определен интеграл стойност зависи само от долните и горните граници и по този начин не зависи от формата на път.

Всички сили не са консервативни, наречена не-консервативните сили. Те включват преди всичко т.нар дисипативни сили, като например сили на триене, възникващи по време на плъзгането на едно тяло спрямо друго.

Силата на триене в този случай е винаги насочени срещу скоростта, която е срещу движението на тялото. Работата на тази сила винаги е отрицателен. И ако тялото се премества наляво, а след това се върна, е ясно, че общата стойност на работата ще бъде отрицателен или нулев. По този начин, на работната сила на триене при движение по затворен контур не е нула!

Фигура 4.5 - Работа триене сила на затворен контур

Като не-консервативни сили да се прилага и устойчивост сили, действащи върху тялото, когато тя се движи в течна или газообразна среда. Тези сили се наричат ​​понякога вискозни сили на триене. За разлика от триене при плъзгане, те винаги са в зависимост от величината на скоростта на тялото и насочен противоположно на него.