конични сечения

коничен

Конусен участък - кривите, получени чрез нарязване на кръгов конус (по-точно - коничната повърхност) не равнина, минаваща през неговия връх.

Полученият по този ограничени стойности са елипси и неограничени (фиг. 1) - хиперболи (ако рязане равнина пресича както кухината на конуса) или параболи (ако рязане равнина пресича само с един от неговите кухини). Всички видове конични части могат лесно да бъдат получени с използване на фенер, насочването от различни ъгли на равен терен. Вярно е, че в хиперболата ние виждаме само един клон. За да видите второто, което трябва факел ос се въртят на 180 °.

Същият метод на получаване включва различни конични секции и сходството на уравнения описват кривите. В равнината на рязане може да изберем координатната система, уравнение на конично сечение има формата, къде и - постоянно. Ако това уравнение определя парабола, когато елипса - ако, хипербола - кога. Геометрична собственост на конични сечения, съдържаща се в горното уравнение, той е бил известен от древногръцкия учен и служи за Аполоний Пергски (около II век пр.) Причина за посочване на отделни видове конични имена секции съществуваха: гръцката дума "парабола" означава " приложението "(както е в гръцката геометрия на тази област в изометрична трансформация правоъгълник правоъгълник с база данни, наречена той прилагането на правоъгълника към базата); думата "елипса" означава "липса" (приложение към долната), думата "хипербола" - "излишък" (с излишък на заявление).

Много подобен на уравненията на конични секции в полярни координати. Ако в продължение на полюса да се кривата на фокус и на полярната ос - ос на кривата, която преминава през фокуса, ние получаваме уравнението

Това е уравнение на елипса в (ако стигнем кръг). Параболата е описан от това уравнение, ако и когато хипербола. Номер нарича ексцентричността на конично сечение, и - за център на параметър.

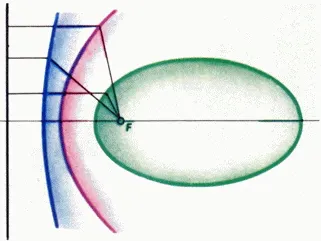
Гръцки математика считат само сечение, перпендикулярно на образуващата на конуса, както и различни видове криви, получени чрез промяна на ъгъла на конус. По-специално, те са установили, че за всеки конично сечение, различно от кръг, в равнината на такава линия съществува за които съотношението на разстоянията на точки на кривата на фокуса на разстоянието от тази права линия е равно на ексцентрицитета на коничната част (фиг. 2). Такава линия е обявен директорка на кривата.

Математически интерес конични сечения е до голяма степен се дължи на факта, че ако напишете уравнението на този раздел в произволна Декартова координатна система на самолета на рязане, тя винаги ще бъде алгебрични уравнения от втори ред, т.е. Тя ще изглежда така:

Обратно, кривата описана от това уравнение е конично сечение, с изключение на случаите, когато коефициентите на това уравнение са свързани с някои отношения.

Всички органи на Слънчевата система се движат около Слънцето по елипси. Небесни тела, попадат в слънчевата система и от други звездни системи се движат около Слънцето по орбита хиперболичен и ако движението им не влияе значително на планетата на Слънчевата система, ето излизат на една и съща орбита. Многоточието, които се движат около Земята на неговите спътници и естествен спътник - Луната и космически кораб стартира към планетите се движат в края на двигателите за параболи или хиперболи (в зависимост от скоростта), докато привличане на другите планети и слънцето не ще привличане сравнима с пръст (фиг. 3).