концепцията за

Начало / математика / концепция на набор. Задайте операции.

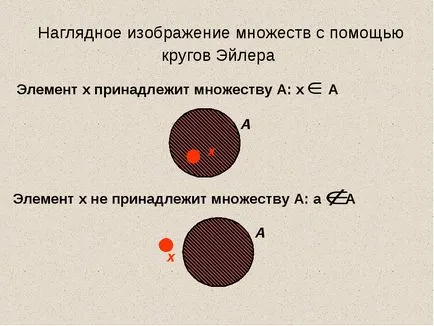
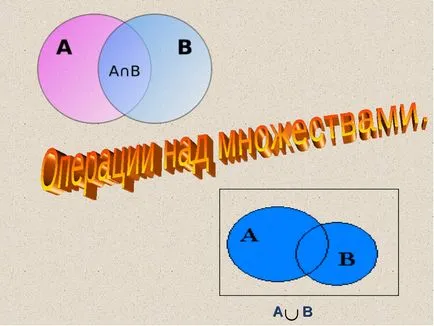
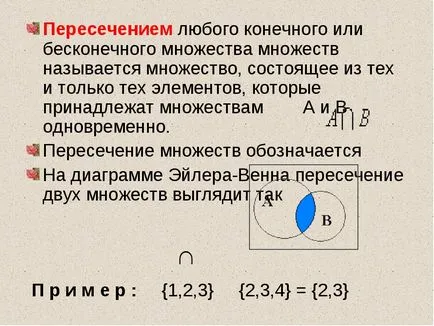
Концепциите на теория на множествата концепция на набор е един от най-често срещаните и най-важни математически понятия. Тя е въведена за математика от немския учен Georgom Kantorom (1845-1918) .Sleduya Кантор, терминът "много" може да се дефинира като: Mnozhestvo- колекция от предмети, които имат определен имот, обединени в едно цяло.

Обектите, които съставляват комплекта се наричат елементи на комплекта. Сред многото откроява много - празен сет. Празни mnozhestvo- Не казвам, съдържащи всеки елемент. В празното множество е част от всеки набор. Примери празно множество. 1) набор от квадратно уравнение, които имат повече от два различни корен; 2) множество от прости делители на 1; 3) комплект пресичането на две успоредни линии на точки; 4) множество ъгли на равностранен триъгълник; 5) много хора на Слънцето; 6) множество от двойни положителни числа разположени отляво на цифровата лъч 9.

Много се счита за сигурен. ако той съдържа всички елементи. Тези елементи могат да бъдат определени с помощта на една обща черта, или чрез използване на списък с която са посочени всички елементи. Mnozhestvo- ограничен набор, състоящ се от краен брой елементи. Endless mnozhestvo- не е празен сет, който не е ограничен.

Пример: набор от естествени числа е безкраен. Подредената набор - набор, всеки елемент се задава определен брой (брой елементи) от 1 до п, където п - брой елементи, така че различните елементи, съответстващи на различни номера. Всеки крайно множество може да се поръча, ако, например, за да копирате всички елементи в списък на някои (а, б, в, г.), А след това присвоите номер към всеки елемент на мястото, където той стои в списъка.

Методи за определяне на множество комплекти от елементите, изброени; Общо описание (характерни) свойства, съчетаващ елементи. Много примери. Използвайки методите на работата си.

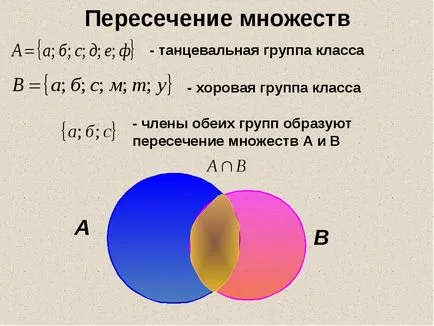
В един клас от 30 души, всеки от които пее или танци. Известно е, че 17 души са песни и танци са в състояние до 19 души. Колко хора са песни и танци в същото време?

Решение. Нека A - много студенти, които знаят как да пее. Броят на елементите в него за същото състояние, п = 17. Под наем - много хора, които знаят как да танцуват. Броят на елементите в него - м = 19. - комплект съвпада с целия клас, защото всеки ученик в класа пее или танци. - набор от членовете на групата, които пеят и танцуват в същото време. (19 17) - 30 = 6 Отговор: 6 студенти в пеенето на класа и танци в същото време.

Всеки студент в класната стая изучаването на английски или френски език. Английски се преподава 25 студенти, френски - 27 ученици и две езикови - 18 студенти. Колко ученици в един клас? Решение: Нека Много от учениците учат английски, F - много студенти, които учат френски, О - много от учениците са английски и френски език. 25-18 = 7 (. Ох) - научете само на английски език; 27-18 = 9 (UCH.) - Френска изследване само; 3) 18+ (7 + 9) = 34 (UCH) А :. ученическа в класа на 34.