Концепцията на три вектори
17) смесен продукт на вектори. Имоти и геометрично значение. Копланарни вектори.
Вектори nazyvayutsyakomplanarnymi. или ако те се намират в една и съща равнина или в успоредни равнини.
Свойства на смесения продукт.
1) смесен продукт [AB] с е равен на обема на паралелепипеда, образувана от горната обща даден векторите на а, Ь, с, когато те образуват дясна ръка или номер, срещу този обем, когато ABC - ляво тройна. Ако, Б и В са в една равнина, а след това [AB] С = 0.
а) Ако, Б и В са в една равнина, а след това векторът [AB] равнина, ортогонална на векторите на А и В, и следователно, [AB] С. Следователно, [AB] С = 0.
в) Ако, б, в, не са в една равнина, [аб] с = | [аб] || в | = S # 903; | в | защото # 966;, където # 966; - ъгълът между а и [AB]. След това | в | защото # 966; - височината в процес на разглеждане от кутията. Така [AB] с = V, където изборът на знака зависи от ъгъла между а и [AB]. Твърдението е доказано.
В действителност, двете страни са обема на същия perellelepipeda. Следователно, позицията на вектора на скоби в смесения продукт не е от значение, и предназначение скоби не са. ABC.
Доказателство. С помощта на координатната влизане скаларен и векторен продукт, ние можем да напишете:
[Ab] в = (Ya Zb - Yb Za) Хе + (ХЬ Za - Ха Zb) Yc + (Ха Yb - Хб Ya) Zc =
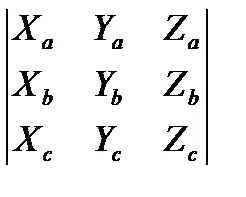
Пример 1. Намираме скаларна тройна продукта от вектори А =, б =, с =. За да направите това, ние се изчисли определящ фактор за тяхното koodinat:
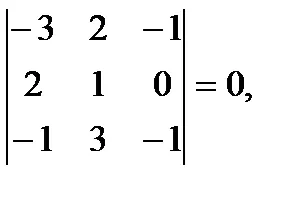
Полярна координатна система