Концепцията на детерминанта п-ти ред

Детерминанта на п-тия ред

Определящ фактор, определящ или п-ти ред е броят да бъдат в писмена форма

и се изчислява според цифрите (реален или сложни) - определящите елементи

Схема изчислителна детерминанти 2ро и 3то поръчки

Нека (делта) е детерминантата на матрична система, и (б) I-детерминанта на матрица, получена от матрицата чрез заместване на й-тата колона на свободната chisel.Togda колона ако (делта) не е равно на 0, системата е еднозначно определена в формула:

1.Opredelitel втория ред се изчислява по формулата

2. детерминанта на третия ред се изчислява по формулата

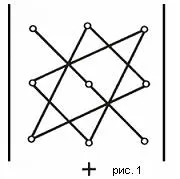
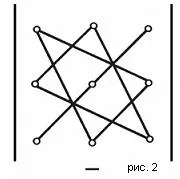
Има удобна схема за изчисляване на детерминантата на третия ред (вж. Фиг. 1 и фиг. 2).

1. Ако някой ред (колона) матрица се състои от всички нули, тогава детерминанта е равно на 0.

2. Ако всички елементи на всеки ред (колона) на матрицата, умножена по Chilo (ламбда) е детерминантата се умножават по този номер (ламбда).

3. При транспониране на детерминантата не се променя матрицата.

Въвеждане - в математиката, тази трансформация матрица квадратни замяна колона в ред или обратно.

4. При транспониране на два реда (колони) детерминантата на матрицата променя знака.

5. Ако квадратен матрицата съдържа две идентични ред (колона), тогава детерминанта е равно на 0

6. Ако елементите на двата реда (колони) на матрицата са пропорционални, че детерминанта е равно на 0

7.Summa продукти от елементи на един ред (колона) матрични кофактори елементи от друг ред (колона) на тази матрица е 0

8.Opredelitel матрица не се променя, ако елементите на ред (колона) матрица за добавяне на елементи от друг ред (колона), предварително умножени по същия номер.

9.Summa продукти от номера В1, В2. млрд да алгебрични допълнение всяка елементи ред (колона) е равна на детерминантата на матрицата, получен от това чрез замяна на елементи на този ред (колона) В1, В2. млрд.

10.Opredelitel продукт на две квадратни матрици е продукт на тяхната детерминанти | С | = | А | * | B |, където С = А * В, А и В са матрици п-ти ред.