комплексно число

Комплексни числа [1] - разширяване на набора от реални числа. обикновено означен \ (\ mathbb \). Всяко комплексно число може да се представи като формално сума \ (х + Iy \), където \ (х \) и \ (у \) - реални числа, \ (и \) - имагинерна единица. че е един от номерата, които отговарят на уравнение \ (I ^ 2 = -1 \). Общоприето произношение е сложен номер. въпреки че произношение комплекс брой също е намерен.

Комплексни числа форма алгебрично затворено поле - това означава, че степента на полином \ (п \) с комплексни коефициенти има точно \ (п \) комплексни корени, т.е. правилна основна алгебра теорема.

Определения [цитат]

Стандартна [цитат]

Формално, комплекс броя \ (Z \) - е подредена двойка реални числа \ ((х, у) \) с въведената тях, както следва присъединителни и умножение операции:

В имагинерна единица в такава система, представено с чифт \ (I = (0,1) \, \). Следователно, погрешно определяне на броя \ (I \) като единствените номера отговарят на уравнение \ (I ^ 2 = -1 \), тъй като броят \ ((-i) \) удовлетворява това уравнение. Трябва също да се отбележи, че експресията на форма \ (I = \ SQRT \) неправилно. като алгебрични корена се определя върху набор от не-отрицателни числа.

Matrix [цитат]

Комплексни числа също може да се определи като едно семейство на реални матрици от формата $$ \ започне х г \\ -y \; \; х \ край $$ с обичайната добавянето на матрица и размножаването. Действителната устройството ще се побере $$ \ започне 1 0 \\ 0 \; \; 1 \ край $$. имагинерна единица - $$ \ започне 0 1 \\ -1 \; \; 0 \ край $$

Всички тези определения водят до изоморфни разширения на реалните числа \ (\ mathbb \), като всеки друг полином разширения поле структура x² 1

Действие на комплексни числа [редактиране]

Още определяне [цитат]

Комплекс променлива обикновено е означен \ (Z \). Нека \ (х \) и \ (у \) са реални числа, така че \ (Z = х + Iy \). след това

Представяне на комплексни числа [редактиране]

Алгебрични форма [цитат]

Записване на комплексно число \ (Z \) на \ (х + Iy \) \ (х, у \ в \ mathbb \), наречен алгебрична форма на комплексно число.

Сумата и продукта на комплексни числа може да се изчисли директно чрез умножаване и сумиране такива термини, като се вземе предвид идентичност \ (I ^ 2 = -1 \).

Тригонометричните и експоненциална форма [цитат]

Ако реално \ (х \) и имагинерна \ (у \) на комплексно число, изразено по отношение на единица \ (R = | Z | \) и аргумент \ (\ varphi \) (\ (X = R \ защото \ varphi \), \ (у = R \ грях \ varphi \)), комплекс броя \ (Z \) могат да бъдат написани в тригонометрични формата $$ Z = R (\ защото \ varphi + I \ грях \ varphi). $$ може също да бъде полезен следната нотация на комплексни числа, е тясно свързано с тригонометричните условията на формула $$ Z = ре ^ Ойлер, $$ където \ (д ^ \) - експоненциално разширение за случай на комплекс експонента.

Геометрично представяне [редактиране]

Ако на Х-ос равнина е реалната част, а вертикалната ос - въображаемото, комплекс броя ще съответства на точка с декартови координати \ (х \) и \ (у \) (или радиус вектор, който е същият) и модул и аргументът ще бъде полярните координати на точката.

Геометричното представяне на комплексни числа съответства на сумата от векторната сума на съответните вектори. Когато се умножи комплексни числа, умножени се добавят своите модули и аргументи. Следователно, по-специално, ние получаваме формула Moivre.

Формулата позволява да се изгради силата на комплексно число представени в тригонометрични форма. DeMoivre формула има формата: $$ Z ^ п = [R (<\href<\texttip <Косинус>>> \ varphi + I \ грях \ varphi)] ^ п = R ^ п (\ п \ varphi защото + I \ грях п \ varphi), $$

Джордж Александров намери най-общата форма на формула DeMoivre на: $$ (х + у \, I) ^ п = \ SQRT \ Bigg [\ защото \ Bigg (\ фракционатор \ Frac \ Frac + п \ operatorname> \ Bigg) + I \ \ Frac \ грях \ Bigg (\ фракционатор Frac \ Frac \ + п \ operatorname> \ Bigg) \ Bigg] $$

където X, Y, п - всяко реално число.

Конюгат на [правило]

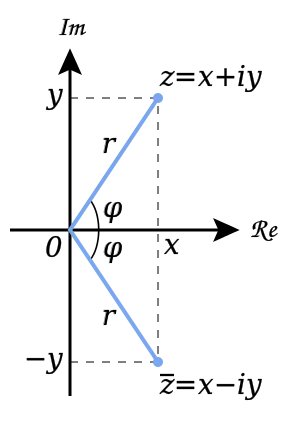
Геометрично представяне на конюгатни номера

История [редактиране]

За първи път, както изглежда, въображаеми количества се появиха в известния работата "Голямото изкуство, или алгебрични правила" Кардано (1545), които са намерили това, негодни за консумация.

Полза на въображаеми количества, по-специално, в решението на квадратното уравнение,, т.нар който не може да бъде принуден случай (когато са изразени по отношение на реалните корени на кубични корени на имагинерни стойности), първо оценява Bombelli (1572). Той също така даде някои прости правила за операции с комплексни числа.

Изрази от вида \ (а + б \ SQRT \), появяващи се в решаването на квадратни и кубични уравнения, станали известни като "въображаеми" в XVI -XVII вековете, но дори и за много от най-големите учени на алгебрични на XVII век и геометричен характер на въображаеми количества е неясно. Известно е, например, че Нютон не включва стойността на концепцията за имагинерни числа, и Лайбниц принадлежи фразата: "Въображаеми номера - това е един голям и прекрасно убежище на божествения дух, почти амфибия съществуване от нищото" [Източник? ].

Проблемът на експресията на корените на степен \ (п \) на даденото число е основно решен в DeMoivre (1707) и Coats (1722).

Символ \ (I = \ SQRT \), предложена от Ойлер (1777 обн. 1794), който го взе за първата буква на думата imaginarius. Той заяви в 1751 идеята за затварянето на алгебрични областта на комплексни числа. Същият извод се стигаше по D'Даламбер (1747), но първата строго доказателство за този факт принадлежи на Гаус (1799). Гаус и въведена в широка употреба ", комплекс брой" е през 1831 г., въпреки че терминът е използван в същия смисъл, както френския математик Лазар Карно през 1803.

Геометрична интерпретация на комплексни числа и операции по тях за първи път в работата на Wessel (инж.). (1799). Първите стъпки в тази насока са направени Wallis (England) в 1685.

Средноаритметичната теорията на Хамилтън (1837) е построена комплексни числа като двойки от реални числа. Той също принадлежи към обобщение на комплексни числа - четворки. комутативен алгебра това.