Комплексни числа

Комплексни числа. Комплекс брой е броят на формата Z = а + biabRi2 = -1

Забележка.
Действителният брой на - е реалната част на Z и е означен с = Рез
Действителният брой б - е имагинерната част на Z и е означен б = IMZ
Реалните числа са пълен набор от числа и операции по тях, което изглежда да е достатъчно за решаване на всички задачи от математиката. Но как да се реши това уравнение в реално номера x2 + 1 = 0? Има още едно разширение номера - комплексни числа. Комплексът номера могат да бъдат взети от корените на отрицателни числа.

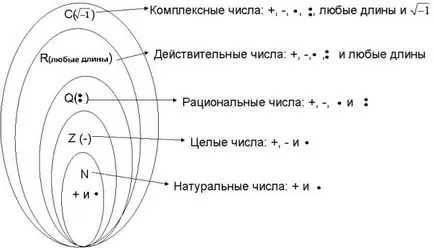
Алгебрични форма на комплексно число. Алгебрични форма на комплексно число има vidz = а + би (aRbRi2 = -1)

Забележка. Ако = Рез = 0b = IMZ = 0, тогава Z се нарича имагинерно число. Ако = Рез = 0b = IMZ = 0, тогава броят нарича чисто въображаема Z

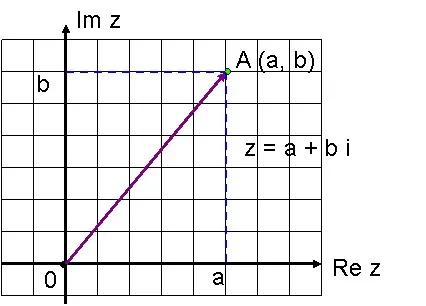
Геометрична интерпретация на реалните числа е истински линия. В допълнение, върху реалната линия "няма място за нови точки", т.е. всяка точка на реалната ос съответства на реално число. Следователно, комплексни числа по тази линия не могат да бъдат позиционирани, но можете да се опитате да се разгледа, наред с реалната ос, на която ще се отложи реалната част на комплексно число, още една ос, перпендикулярна на нея; ние го наричаме въображаемата ос. След всяко Z = + иб комплекс номер може да бъде поставен в съответствие с точка на координатната равнина. По хоризонталната ос ние парцел реалната част на комплексното число, а вертикалната ос - един въображаем част. Това създава една еднозначна между всички комплексни числа и всички точки в равнината. Ако тази линия е изградена, координатната равнина, наречена комплексната равнина. Тълкуване на комплексно число Z = а + б и е вектор OA с координати (а, б) като се започва в точка О, (0,0) и завършва в точка А (а, Ь)

Конюгати. Брой Z = а + Bi, и Z = с-би са спрегнати комплексни числа

Собственост. Сумата и продукта от две комплексни числа конюгатни са реални числа: Z + Z = 2azz = а2 + b2

Добавка обратен. Брой Z = а + BI и -z = -а-би противоположни комплексни числа, наречени.

Собственост. Сумата от две противоположни комплексни числа е нула:
Z + (- Z) = 0

Същия брой. Две комплексни числа се казва, че е равна, ако те са реални и въображаеми части.

Действия с комплексни числа, дадени в алгебрични форма:

собственост на прибавяне: Размер на две комплексни числа Z1 = а + BI и Z2 = С + ди е комплекс броя на формата Z = Z1 + z2 = а + BI + в + ди = а + в + (б + г) и
Пример: 5 + 3i + 3i = 8 + 2i

изваждане на имота: Разликата от две комплексни числа z1 = а + BI и Z2 = С + ди е комплекс броя на формуляра Z = Z1, Z2 = а + двупосочно в + ди = А-С + (б-д) и

умножаване на имота: Продуктът от две комплексни числа z1 = а + BI и Z2 = С + ди е комплекс броя на формуляра Z = z1z2 = а + БИК + ди = ав-BD + (реклама + бв) и

разделяне на имота Self две комплексни числа z1 = а + BI и Z2 = С + ди е комплекс броя vidaz = z2z1 = С + диаметър + BI = с2 + d2ac + BD + С2 + d2bc-ADI

Действия с комплексни числа, дадени в тригонометрични форма

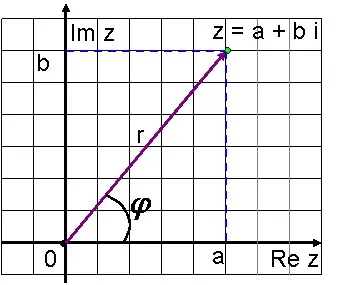
Записване на комплексно число Z = а + би под формата на Z = rcos + ISIN наречен тригонометрични форма на комплексно число.

Модул комплексно число: R = а2 + b2

Аргумент на комплексно число: COS = Расин = RB

Въображаеми и комплексни числа

Помислете за непълно квадратно уравнение:
х 2 = а,
където - известно количество. Решението на това уравнение може да се запише като:
Има три възможности:

1). А = 0. Ако х = 0, тогава.

където а, б - реални числа, аз - имагинерна единица.

ПРИМЕР Пример комплексни числа S 3 + 4 т. 7 - 13,6 т. 0 + 25 25 I = аз. 2 + I.

Запознаване с имагинерни и комплексни числа, вижте "въображаеми и комплексни числа." Необходимостта от нов тип номера се появи в решаването на квадратно уравнение в случай на D
Увеличаването му числител и знаменател от 2 + 3i

и завършени всички промени, получаваме:
Геометрично представяне на комплексни числа. Реални числа са представени с точки на редица линия: където А означава броя на точка 3, точка Б - номер 2 и О - нула. За разлика от комплексни числа са представени от точки на координатната равнина. Ние избираме тази правоъгълна (декартова) координира с една и съща скала върху двете оси. След комплекс номер + bibudet представено с точка Р с абсциса а и б ордината (вж. Фиг.). Тази координатна система се нарича комплексната равнина.

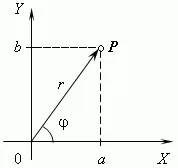
Модулът на комплексно число е дължината на ОП вектор, изобразяващи комплексно число на координатната (комплекс) равнина. сложен номер + двупосочен модул е ​​определен | с + двупосочен | или писмо, и г е равна на:
Конюгираните комплексни числа имат един и същ модул. __

Аргумент на комплексно число - е ъгълът между оста ОХ и ОП вектор, изобразяващи комплексно число. Следователно, тен = б /.

Тригонометрични форма на комплексно число. Абциса а и б ордината на комплекс номер + би може да се изрази чрез модула на R, и аргумент.
Операции с комплексни числа, представени с тригонометрични форма.

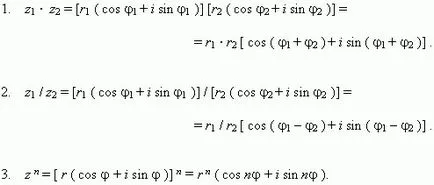
Този прочут формула Moivre.
Тук к - единица. За да се получат различни стойности на корен п п-ти мощност на Z е необходимо да се определят стойности за п последователни к (например, к = 0, 1, 2, ..., п - 1).