Калкулатор онлайн - приравняваме самолет

Този калкулатор е онлайн (намерите) уравнението на равнината от три точки, които се намират в самолета, или нормална и една точка лежи на самолета.

Онлайн калкулатор за намиране на уравнението на самолета не е просто дава отговор на проблема, той дава подробна решение с обяснения, т.е. процес дисплеи за вземане, за да проверят знанията по математика и / или алгебра.

Този онлайн калкулатор може да бъде полезна за студенти от висшите класове на средните училища в подготовка за тестове и изпити, проверка знанията преди изпита, на родителите да следят решенията на много математически и алгебра проблеми. Или може би са твърде скъпи за наемане на преподавател или да купят нови книги? Или просто искате възможно най-бързо, за да си напишат домашното по математика или алгебра? В този случай, можете да се възползвате от нашите програми с подробни решения.

По този начин можете да извършват своята част от обучение и / или обучение на малките си братя или сестри в същото ниво на образование в областта на задачите се увеличава.

Правила въведете номера

Номерата могат да се прилагат или цяло число или фракционна.
Освен това, частични номера могат да се прилагат не само като знак, но под формата на обща фракция.

Правила за въвеждане на десетични дроби.
На десетичните на фракционна част могат да бъдат разделени като цяло точка и разделят.
Например, може да се прилага като десетични знака: 2.5 или така 1,3

Правилник за вписване на фракции.
В само цяло число може да действа като числител знаменател, и цялата част на фракцията.

В знаменателя не може да бъде отрицателен.

При въвеждане на цифров числител на фракцията се отделя от знака на деление знаменател: /
Вход: -2/3
Резултат: \ (- \ Фрак \)

цялата част на фракция се отделя от амперсанд:
Вход: -15/7
Резултат: \ (-1 \ Фрак \)

Тези решения са създадени и съхранени от потребителите на нашия сървър
използването на този онлайн калкулатор.

Общото уравнение на равнина

Да предположим, че:
правоъгълна координатна система Oxyz,
произволно самолет ;
точка ;
вектор , перпендикулярна на равнината (Виж фигурата).

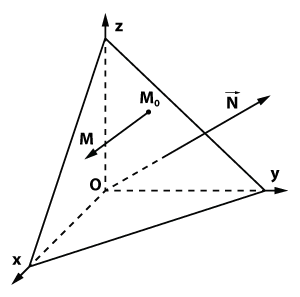
Да разгледаме произволна точка М (х; у; Z). М лежи в равнина, ако и само ако векторите "> и" > взаимно перпендикулярни. . Тъй като координатите на вектор "> са равни с оглед на състоянието на перпендикулярност на двата вектора (скаларното продукт трябва да бъде нула), която точка М (х; у; Z) лежи в равнина, тогава и само тогава

Това е желания уравнението на равнината като х координира това изпълнение; Y; Z всяка точка М, лежи в равнина, и не отговаря на координатите на всяка точка, която не лежи в тази равнина.

Скобите, ние намаляване на уравнение (1) на формата

Освен това, обозначаваща броя през, получаваме

Уравнение (2) е общо уравнение на равнина. Така равнина е повърхността на първия ред, определен от уравнението на първа степен.

Обратно, всяка първа степен уравнение на формата (2) определя равнина в предварително определена правоъгълна координатна система. Наистина, нека определена правоъгълна координатна система Oxyz уравнение с произволни коефициенти А, В, С и D, при което коефициентите А, В и С е най-малко една нула. Това уравнение е известно, че има поне едно решение (ако, например, той взе произволно x0 и y0 от уравнението получаваме: ..).

По този начин, съществува най-малко една точка M0 (x0; Y0; z0), координатите на които отговарят на уравнението, т.е. Ax0 + By0 + Cz0 + D = 0. Изваждане това уравнение от цифровата уравнение Ах + С + D + Cz = 0, ние получаваме уравнението
А (х-x0) + B (у-y0) + C (Z-z0) + D = 0,
еквивалентно на това. Получената уравнение (и следователно, уравнение Ах + на С + Cz + D = 0) съвпада с уравнение (1), и следователно определя равнината, минаваща през M0 точка (x0 и перпендикулярна на вектора (А; В; С) "/ >.

Векторът (А; В; С) ">, перпендикулярна на равнината се нарича нормален вектор и нормалата на тази равнина.

теорема
Ако двете уравнения и определят една и съща равнина, те са пропорционални на коефициенти, т.е.

Ъгълът между двете равнини

Помислете два самолета и е определено от уравненията

Във всеки режим равнините в един от ъглите пространство между тях е равен на ъгъла между техните нормали (A_1; B_1; C_1) "> и (A_2; B_2; C_2)" > и се изчислява по следната формула:

Вторият ъгъл е

Състоянието на успоредни равнини

Ако равнина и успоредно, колинеарна обичайно "> и" >, и обратно. но след това
">
Състояние (4) е състояние на успоредни равнини и

Състояние перпендикулярни равнини

Ако равнина и перпендикулярни една на друга, обичайно "> и" > и перпендикулярно, и обратно. Следователно, от формула (3) директно да се получи състоянието на перпендикулярност на самолетите и:

Книги (книги) Книги (други) изпитни есета и OGE тества онлайн игри, пъзели заговор функции правописен речник на българския език речник на младостта жаргон стоките Училища България Каталог SSUZov България университети продукта в България проблеми с намирането на ГРУ и LCM полином опростяване (умножение на полиноми) на полином деление Изчисляване на полинома на колонни фракции числено решаване на проблемите на интереси Комплекс: сума, разликата, произведението и частното системи 2 линейни уравнения с две променливи Solution квадратно уравнение Изолиране квадратен биномно и факторинг квадратичен полином неравенства решения решение неравенства системи Изграждане на квадратна функция графика изчертаване е линейна фракционна функция решаване аритметика и геометрична прогресия решение тригонометрични, експоненциални, логаритмични уравнения Изчисляване на граници, производно, допирателни интегрални примитивни разтвор триъгълници Изчисленията действия с вектори действия Изчисленията на линия и равнина площ геометрик Месечен периметър оформя геометрични форми геометрична повърхност обем форми на геометрични фигури
Дизайнер ситуации на пътя
Времето - Новини - хороскопи
MathSolution.ru програма на Google Play