Какво е диагонала на куб, и как да го намерите

Какво е куб, и това, което има по диагонал

Cube (редовна полихедронов или шестостен) е триизмерна фигура, всяка страна - това е квадрат, което, както знаем, всички страни са равни. куб диагонал е сегмент, който минава през центъра на фигурата и да се свържете симетрични върхове. В десния шестостен има диагонал 4, и те всички ще бъдат равни. Важно е да не се обърка диагонала на самата фигура с диагонал си лице или квадрат, който се намира в основата му. Диагонал на куба минава през центъра на лицето и се свързва противоположните върховете на площада.

Формула, която може да намерите диагонала на куб

Диагонал редовен полихедронов може да се намери на много проста формула, която искате да запомните. D = a√3, където D представлява диагонала на куба, и - този ръб. Ето един пример на проблема, когато е необходимо да се намери диагонал, ако знаете, че тя е равна на дължината на ръба на 2 см. Толкова е просто D = 2√3, дори не е необходимо да се разгледа всичко. Във втория пример, да ръба на куб е равно на √3 см, след което се получи D = √3√3 = √9 = 3. Отговор: D е равно на 3 см.

Формула, която може да намерите диагонала на куба

Диаго

Nahl аспекти могат да бъдат намерени по формулата. Диагонали, които се намират върху лицата на само 12 парчета, а те всички са равни. Сега си спомням г = a√2, където г - е диагонала на квадрат, и - това е също един куб ръб или край на площада. За да се разбере къде тази формула е много проста. В крайна сметка, от двете страни на квадрата и диагонал формата на правоъгълен триъгълник. Това трио играе ролята на диагонал хипотенуза и край на площада - това е на краката, които са с еднаква дължина. Нека си припомним, Питагоровата теорема, а всички наведнъж ще си дойде на мястото. Сега проблем: ръба шестостен равнява √8 видите, че е необходимо да се намери диагонал на лицата си. Вмъкната във формулата, и ние получаваме D = √8 √2 = √16 = 4. Отговор: По диагонала на куба е 4 см.

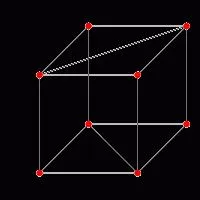
Ако знаем, лицата на куба диагонал

Според изявлението на проблема, ние се дават само диагоналните лицата на регулярна полихедронов, което е равно на, да речем, √2 см, а ние трябва да намерим диагонал на куб. Формулата за решаване на този проблем е малко по-сложно предишния. Ако знаем, г, а след това можем да намерим на ръба на куба, въз основа на втората ни формула г = a√2. Получаваме = г / √2 = √2 / √2 = 1 см (това е нашата страна). И ако знаем, тази стойност, а след това намери куба диагонал не е трудно: D = 1√3 = √3. Ето как разрешихме задача.

Ако известна площ

Следващият алгоритъма се основава на намирането на решения по диагонал над повърхността на куба. Да предположим, че е 72 cm 2. За да намерите началото на площ от едната страна, а общо 6. След това, 72 трябва да бъде разделена на 6, ние получаваме 12 cm 2. Тази област на едно лице. За ръба на редовен многостен, е необходимо да се припомни формула S = а 2 означава = √S. Заместител и получи = √12 (куб ръб). И ако знаем, тази стойност, и не е трудно да се намери диагонал D = a√3 = √12 √3 = √36 = 6. Отговор: Диагоналът на куб е равно на 6 cm 2.

Ако е известен дължина куб ръбове

Има случаи, в които проблемът е даден само от дължината на всички ръбове на куба. След това е необходимо да се разделим на 12. Това е броят на страните в редовен polyhedra. Например, ако сумата на всички ръбове е равно на 40, от едната страна ще бъде равна на 40/12 = 3333. Ние поставяме в нашата първа формула и да получите отговор!