Как да сортирате фракции качваха

3 Процедура: произволен брой drobeyDve фракция (чрез умножаване на кръст) Неправилно фракция

Метод 1 от 3: произволен брой фракции

1. 
   1 Намери общ знаменател, който ще ви позволи да поръчате произволен брой фракции. Можете да намерите общ знаменател, или най-малкия общ знаменател (ЕНП). За тази цел се използва един от следните методи: [1]
   • Умножете различни знаменатели. Например, ако се поръча фракции 2/3, 5/6, 1/3, умножете две различни знаменател: 3 х 6 = 18. Това е прост начин, но в повечето случаи няма да намерите Ноу.
   • Или пишете кратни на всеки знаменател, и след това изберете номер, който се появява в списък на всички кратни. В този пример, броят на кратни на 3 са 3, 6, 9, 12, 15, 18; кратни на 6 са: 6, 12, 18. Тъй като броят на 18 е намерена и в двата списъка, това е общият знаменател на тези фракции (ERA = 6 тук, но ние ще работим с номера 18).
2. 
   2 Дайте всяка фракция под общ знаменател. За тази умножаване на числителя и знаменателя на броя равна резултат от разделяне на знаменател общ знаменател за специфични фракции (обърнете внимание, че когато се умножи числителя и знаменателя на фракция номер едно стойност не се променя). В нашия пример, да фракции 2/3, 5/6, 1/3 18, под общ знаменател.
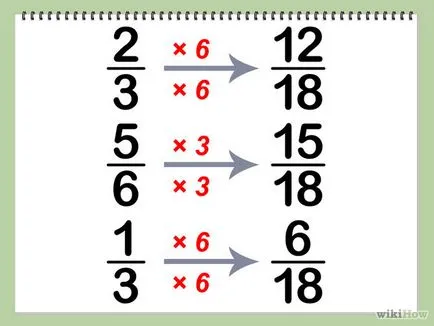
   • 18 ÷ 3 = 6, следователно 2/3 = (2x6) / (3x6) = 12/18
   • 18 ÷ 6 = 3, така че 5/6 = (5x3) / (6x3) = 15/18
   • 18 ÷ 3 = 6, следователно 1/3 = (1x6) / (3x6) = 6/18
3. 
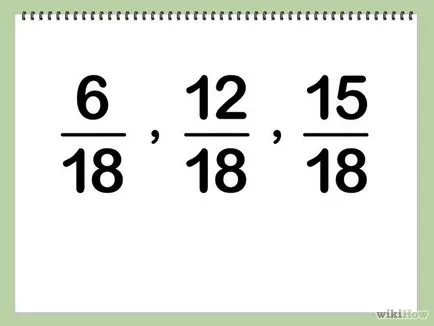
   Подреждане на три фракции според техните числители (от най-малката до най-голямата). В този пример правилния ред е: 6/18, 12/18, 15/18.
4. 
   4 Не промените реда на фракции, напишете ги в оригиналния им вид. За да направите това, да ги опрости, разделяне на числителя и знаменателя на съответния брой.
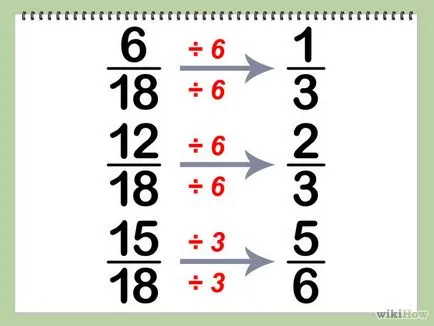
   • = 6/18 (6 ÷ 6) / (6 ÷ 18) = 1/3
   • 12/18 = (12 ÷ 6) / (6 ÷ 18) = 2/3
   • 15/18 = (15 ÷ 3) / (18 ÷ 3) = 5/6
   • Отговор: 1/3, 2/3, 5/6

2, Метод 3: Две фракции (чрез умножаване на кръст)

1. 
   1 Запишете две фракции съседни един на друг. Например, 3/5 и 2/3, организира фракция. От ляво на пиша 3/5, 2/3 и в дясно.
2. 
   2 размножава числителя от знаменател от първата фракция на втората фракция. В нашия пример, се размножават числителя на първата фракция (3) от знаменател на втората фракция (3): 3 х 3 = 9.
   • Този метод се нарича "умножаване на крос-мъдър", защото те умножи броят разположен по диагонал.
3. 
   3 Напишете резултата за първата фракция. В нашия пример, пиша за 9 3/5 (вляво).
4. 
   4 размножава числителя от знаменател на втората фракция от първата фракция. В нашия пример: 2 х 5 = 10.
5. 
   5, за да запишете резултата на втората част. В този пример, публикувайте 10 около 2/3 (вдясно).
6. 
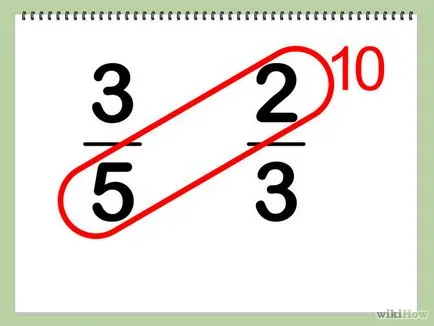
   6 Сравняване на получените резултати. В този пример 9 е по-малко от 10, така до 9 фракция (3/5) 10 до малък фракция (2/3).
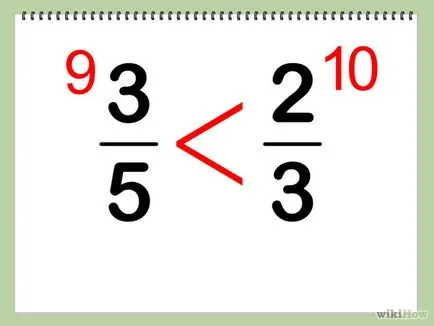
   • В резултат от умножението винаги пиша в непосредствена близост до вратата, но тя е на числителя.
7. 
   7 Обяснението на този метод. За организиране на двете фракции е необходимо да ги доведе до общ знаменател. Така умножи на кръст и води две фракции под общ знаменател! [2] Ето, ние просто не пишете знаменателите, тъй като те са едни и същи, и веднага сравни числителя. Тук е нашият пример, без да се умножи крос-мъдрите:
   • 3/5 = (3x3) / (5x3) = 9/15
   • 2/3 = (2x5) / (3x5) = 10/15
   • По този начин, по-малко от 3/5 2/3.

Метод 3 от 3: Неправилни фракции

1. 
   Неправилното фракция 1 - фракция чийто числител е по-голямо от или равно на знаменателя, например, 8/3 или 9/9 (т.е. стойността на фракция, равна на или по-голяма от един). [3]
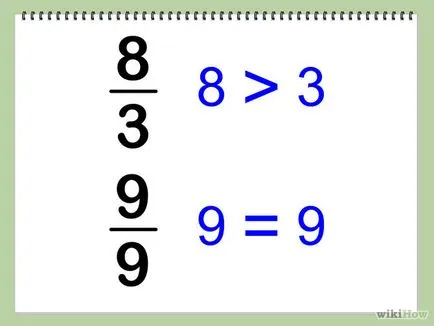
   • Можете да използвате други методи за неправилни дроби. Въпреки това, на описания метод е проста и бърза.
2. 
   2 Конвертиране всяка фракция в погрешна смесен число. Смесени брой - запис тип неправилни фракции, съдържащи число и фракционни части. Можете да направите това в предвид (например 9/9 = 1) или чрез използване на разделение. В резултат на разделяне на цялата част е писано в смесен броя и остатъкът - в числителя на дробна част (знаменател не се променя). Например:
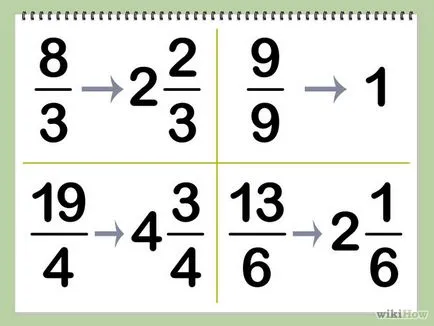
   • 8/3 = 2 + 2/3
   • 9/9 = 1
   • 19/4 = 4 + 3/4
   • 13/6 = 2 + 1/6
3. 
   3 Първо, организира смесени номера от техните целочислени части (около фракции от време за сигурен).
   • 1 - най-малък номер.
   • 2 + 2 + 2/3 и 1/6 - тук ние не знаем кои от тези смесени числа вече.
   • 4 + 3/4 - най-големият смесено число.
4. 
   4 Ако две еднакви числа смесен цялата част, да сравните дробна част, с което в миналото под общ знаменател. В нашия пример, ние смесват 2 бр 2/3 + 1/6 + 2 и сравняват дробни части:
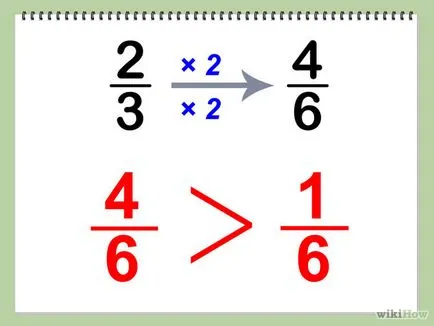
   • 2/3 = (2x2) / (3x2) = 4/6
   • 1/6 = 1/6
   • 4/6 повече от 1/6
   • 2 + 4/6 + 1/6 е по-голямо от 2
   • 2 + 2/3 + 1/6 над 2
5. 
   5 Организиране на смесени числа във възходящ ред. В този пример, 1, 2 + 1/6 2+ 2/3 4+ 3/4.
6. 
   6, без да променя реда на смесени числа, да ги конвертирате обратно в грешната фракция. В нашия пример: 9/9, 8/3, 13/6, 19/4.

• Ако са дадени много фракции, да сравните и да ги организирате чрез разбиване на малки групи (2, 3, 4 фракции).
• Ако същите фракции числителите, а след това да ги запишете в ред, като се започне с по-голям знаменател, например, 1/8 <1/7 <1/6 <1/5.
• Приемливо е да сравни фракции, привеждането им под общ знаменател (т.е., потърсете най-малкия общ знаменател не е необходима). Опитайте се да рационализира фракция 2/3, 5/6, 1/3, като се използва общ знаменател 36, - вие получавате същия резултат.