Как да се парцел графиката на модула за функция и корена

Разглеждане функция у = │ah │, където А - определен брой.

Домейнът на функция у = │ah │, е съвкупност от реални числа. Фигурата показва графики съответно funktsiyu = │h │, у = │ │ 2, у = │h / 2│.

Може да забележите, че графиката на у = | ах | получена от графиката на функция у = ос. ако отрицателната част на графиката на у = брадва (е под х-ос), отразява симетрично на тази ос.

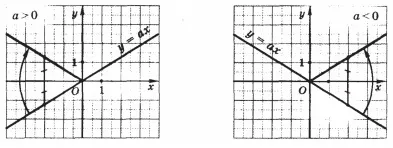
Според графика е лесно да се види свойствата на функцията у = брадвата │ │.

Когато х = 0, у = 0 получаваме, това е, принадлежи на графиката на произход; при х = 0, имаме у> 0, т.е. всички други графични точки лежат над оста х.

За стойности на х обратното. стойности трябва да бъдат еднакви; Y-оста е оста на симетрия на графиката.

Например, може да се построи крива на функция у = 3 │h │ а. С цел да се сравни функция Y = │h │i 3 у = х 3 грим таблица на стойностите за същите стойности на аргументи.

От таблицата се вижда, че за да се конструира крива на функция у = 3 │ │h, може да започне с изграждането на графиката на у = х 3. След това означава симетрична ос Ox показват, че част, която е под тази ос. Като резултат, ние получаваме на графиката, показана на фиг.

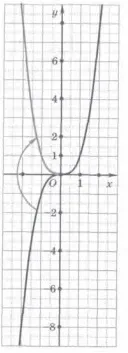
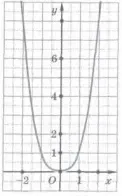
Да разгледаме функция у = х 1/2.

Областта на тази функция е набор от неотрицателни реални числа, тъй като изразът х 1/2 има стойност само тогава, когато х> 0.

Ние изграждане на графика. За да се състави таблица на ценностите си с помощта на калкулатора, закръгляването на стойностите на функцията до десетия.

След нанасяне на точките на координатната равнина и гладка техните съединения, ние получаваме графика funktsiiu = х 1/2.

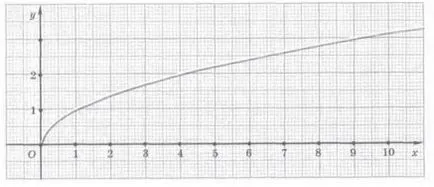
Снабдяване ни позволява да се формулират някои свойства на функция у = х 1/2.

Когато х = 0, получаваме у = 0; за х> 0, ние Y имат> 0; графика преминава през произход; останалите точки на графиката намира в първата координатна тримесечие.

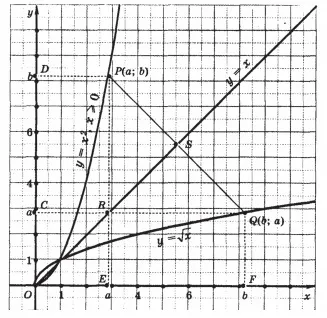
Доказателство. Графиката на функция у = х 2 където х> 0, парабола клон, разположен в първата координатна тримесечие. Нека точка Р (а, б) - произволна точка от тази графика. След това, вярно равенство и б = 2. Тъй като състоянието на не-отрицателно число, също така е вярно равенството а = б 1/2. Това означава, че координатите на точка Q (б; а) се превръща в формулата у = х 1/2 в истинско равенство, или по друг начин, точка Q (б; а) принадлежи към графиката на функция у = х 1/2.

Също така е доказано, че ако точка М (С; г) принадлежи към графиката на функция у = х 1/2. точката N (г; и) принадлежи към графика Y = х 2 където х> 0.

Оказва се, че всяка точка Р (А; б) от графика Y = х 2 където х> 0, съответства на уникален точка Q (б; а) на графиката на функция у = х 1/2 и обратно.

Остава да се докаже, че точка Р (а, б) и Q (б, с) са симетрични по отношение на линията Y = Х. Понижаването вертикалите на координатните оси на точки P и Q. получаване на тези оси точка Д (а 0), D (0; б), F (б 0) C (0, а). Точка R на пресичане на вертикалите и PE QC има координати (а, а) и следователно принадлежи към линията Y = х. PRQ е равнобедрен триъгълник, защото му страни са RP и RQ │ б - и всеки │. Y = х права линия пресича ъгъл като DOF. и PRQ ъгъл и пресича сегмент PQ до определена точка С. Следователно, сегмент RS пресича PRQ триъгълник. От симетралата на равнобедрен триъгълник е неговата височина, а медианата, PQ ┴RS и PS = QS. Това означава, че точката Р (а, б) и Q (б, с) са симетрични спрямо линията Y = х.

От графиката на функция у = х 1/2 симетричен графики функция у = х 2 където х> 0, спрямо линията Y = х. след това графиката на у = х 1/2 е клон на параболата.