Как да разширите биномиално факторинг

Нютонов - алгебричен израз с две понятия, свързани със знак плюс или минус. Един от членовете трябва да включва променлива, а другият може да го включи или не (т.е. може да бъде свободен член). Разлагането двучленни средства намирането на членовете factorizations така, че когато се умножава резултат на първоначалния биномните. процес на разлагане зависи от началния биномните член.

Част 1 от 4: Определяне биномно разширяване метод факторизиране

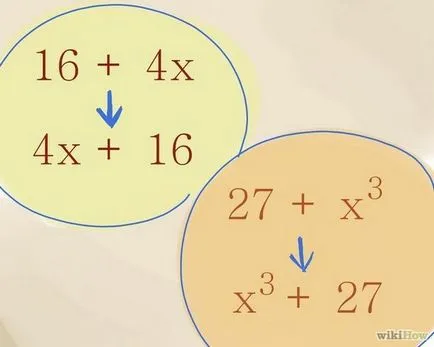
Организирайте членове. Записване биномно като 16 + 4 е priemlemoy- обаче, в повечето случаи, членове на всички полиноми (включително binomials) се записват, като се започне с термина съдържащ висока променлива ред. По този начин, по-горе по-правилно написана като биномиално 4x + 16 и 27 + х биномиално двете х + 27.

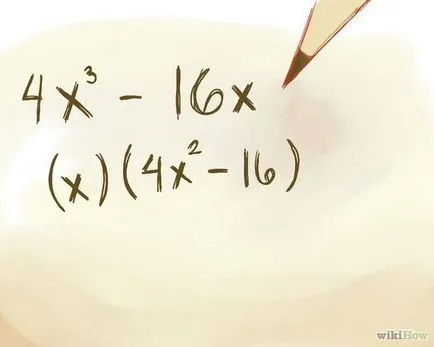
Един или двама членове с промяната. Ако и двете член на биномно съдържа променлива, тогава трябва да вземе това под внимание. При разширяване на биномно променлива се изважда от скобите.

Например, ако източникът е биномно формата х - 3X, вземат променливата "х" на конзолите: х (х - 3). Ако източникът е даден от биномно х + 60x, извадете променливата х на скоби: X (х + 60).

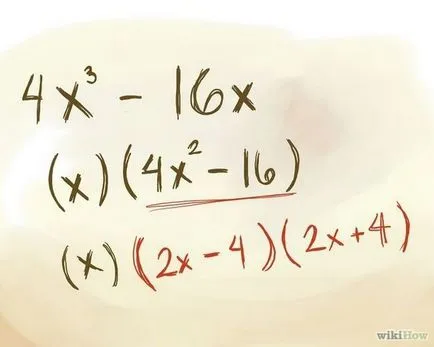
Погледнете нивото на променливата. Той определя стойността на метода на биномно факторизиране експанзия.

Намерете най-голям общ делител (ГРУ) на коефициента на променливата и в по-свободен член. Коефициент - номер, който стоеше peremennoy- свободен член - променлива, която не съдържа променлива. Например, в 2х + 9 Биномен коефициент е 2, и постоянната Терминът равна на 9. Ако в променлив фактор не, то тогава е 1.

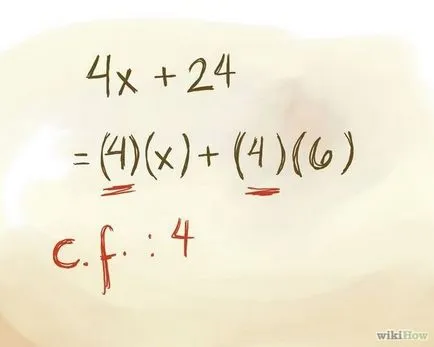
Например, за биномно 2х + 8 = Нод 2. За биномно 4x - 16 Нод = 4.

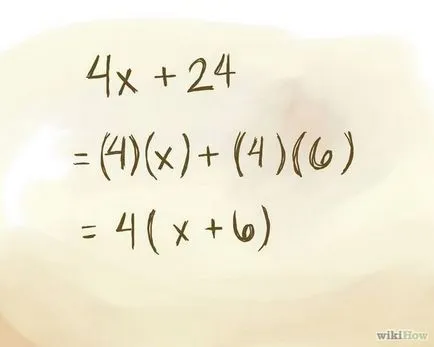
Разделете коефициент и постоянното термин в NOD и NOD извадят от скобите.

Например, 2х + 8 = 2 (х + 4). Например, 4x - 16 = 4 (х - 4).

За биномно, който съдържа и двата термина променливи, извадете скобите като GCD и променлива (нисш ред). Например, за биномно 3x - 9х GCD = 3, а долният ред има променлива "х". Ето защо, ние извадете скобите 3x. По този начин, 3x - 9х = 3x (х - 3). Част 3 от 4: разпадане на квадрати разлика

Уверете се, че коефициентът и постоянното план са перфектни квадрати. Ако степента на променливата е равно на 2 или кратно на 2 (х, х, х и т.н.), уверете се, че коефициентът и постоянното терминът е точен квадрат (т.е. корен квадратен от тях могат да бъдат отстранени).

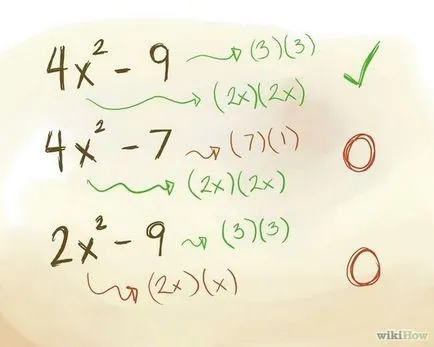
В биномно (4х - 9) 4 е идеален квадрат (2 * 2 = 4) и 9 е идеален квадрат (3 * 3 = 9), обаче, този биномно да бъдат отчетени.
Тригонометрично (4x - 7) 4 е точен квадрат (2 * 2 = 4), 7, но не и точен квадрат, така че това не може да бъде биномиално предупреждавам.
Тригонометрично (2х - 9) 9 е точен квадрат (3 * 3 = 9), но 2 не е точен квадрат, така че това не може да бъде биномиално предупреждавам.
Имайте предвид, че ако има с променлива скорост, това е равно на 1, което е точен квадрат (1 * 1 = 1).

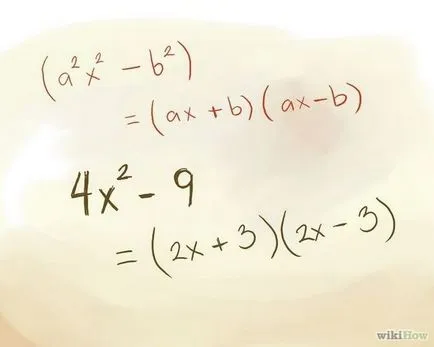
Спред между квадратите на факторите на формуляра: (брадва + б) (брадва - б), където "а" - коефициент стойност (равна на квадратния корен на източника на коефициент биномиално), «б» - безплатно термин стойност (равна на квадратния корен от свободен изходен елемент биномно).

Нютонов 4x - 9 разлага следните фактори: (2х + 3) (2х - 3).

Биномните х - 256 се разлага в фактори два пъти. Първият разлагане от (х ^ 2) ^ 2 = х ^ 4 и 16 ^ 2 = 256, тогава X - 256 = (х + 16) (х - 16).

Вторият разлагането са получени биномно (х - 16), - разлика от квадрати, която се разделя на (х + 4) (х - 4), х - 256 = (х + 16) (х + 4) (х - 4 ). Част 4 от 4: Factoring сумата или разликата на кубчета

Уверете се, че коефициентът и постоянното план са пълни кубчета. Ако степента на променлива е кратно на 3 или 3 (х, х, х, и т.н.), се гарантира, че коефициентът и постоянен план са пълни кубчета (т.е. може да се екстрахира в основата на трета степен).

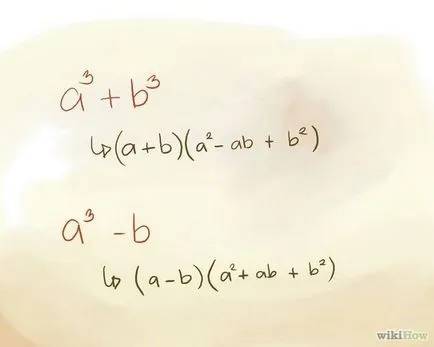
Определя член на знак между променлива и постоянна план (плюс или минус). Знакът зависи от начина, по който биномиално разширяването.

Ако постоянно терминът се добавя към променлив елемент: (ос + б) = (ос + б) (A - ABX + В). Например, х + 27 = (х + 3) (х - 3x + 9).

Ако постоянно терминът се изважда от променливата член: (A - б) = (A - б) (брадва + ABX + Ь). Например, х - 27 = (х-3), (х + 3x + 9).

В някои случаи, в резултат на трином може да намери израз.

предупреждения

Сумата от квадратите могат да бъдат отчетени с помощта на имагинерните числа.

Внимание, само днес!