Изпълнението на симплекс метода

Така че, в лявата колона са написани основните (основни) променливи, всички променливи на проблема, са изброени в първия ред на таблицата. В най-дясната колона съдържа постоянни условия b1 ограничение система. b2. BM. В последния ред на таблицата (наречена очакваните) съхраняват коефициентите на обективната функция и стойността на обективната функция (с противоположен знак) като текущия основен разтвор L = -f (х). Работната част на масата (започвайки от втория ред и втората колона), изброени коефициентите Aij с променлива система ограничение.

ЗАБЕЛЕЖКА! Преглед на маса може да бъде различна, но това не променя работния процес.

В първия основен разтвор свободните променливи x1. .... хп е равна на нула. Основни променливи са различни от нула и може да бъде получена като резултат от ограниченията на разтвора: Xn + 1 = В1; Xn + 2 = b2; ...; Xn + m = BM. Този основен решение е валидно. Естествено, стойността на обективната функция в този случай е равно на нула, както и в образуването на обективната функция, включващи променливи, че за база разтвори са малцинство.

4 Условия на изпитването: всички CJ ≤ 0. Ако "НЕ" - преход към стъпка 5, ако "ДА" - проблемът е решен. По този начин, този етап проверки за положителни елементи в последния ред на таблицата на симплекс. Ако са необходими такива елементи, за да продължи на решението.

5 Изберете разделителната колона (променлива въведена в база). Оставя колоната избран в съответствие със следното условие: CR = maxcj>, J = 1, ..., п + т, където R - брой решаване колона. По този начин, при определяне на колоната позволява да гледате на последния ред на таблицата на симплекс и в нея се търси най-положителен елемент.

6 Условия на теста: всички въздух ≤ 0. Ако "ДА" - целевата функция е неограничено, и там не е решение, ако "не" - преминете към стъпка 7. Трябва да се провери елементите, които позволяват на колоната. Ако никой от тях не е положителен, тогава проблемът е нерешим.

7 Избор решаване низ (променлива мощност от базовата линия) при следното условие:

за въздух> 0, където S - брой резолюция линия.

Така, тези редове, където елементите, позволяващи положителен колона, е необходимо да се намери коефициент елемент BI на (последната колона на таблицата) от елемент, разположен в колоната за освобождаване. Като избран резолюцията, на реда, за които в резултат на това разделение ще бъде най-малкият. Елемент в пресечната точка на линия резолюция и позволява на колона, наречена толерантен член.

8 Брой на членовете на таблицата на симплекс (преход към нов основен разтвор).

За елементи разделящи низ използва следната формула:

където S - разделящи брой ред, г на - брой разделяне колоната. - Нови стойности се преизчисляват елементи, asj. BS - нова стойност се преизчисляват елементи, ASR - нова стойност позволява елемент. При преобразуване линия елементи за разрешаване на всеки елемент, разделен позволява елемент.

Елементите, които позволяват на колоната с изключение на разделителната елемент, който е 1, са нулеви: = 0,

Елементи, които не са собственост на разрешителни колони и редове. преведените използва т.нар правило правоъгълника: психически подчертано правоъгълник, в която елемент да се преизчислява, и позволява на елемента за да се образува един от диагоналите. Формула ще бъде както следва:

където, - новите стойности са преведени елементи

Aij. двупосочно. CJ. L - стара стойности се преизчисляват елементи.

Работа с таблицата за симплекс

Първият симплекс таблицата претърпява трансформация, същността на което е да се премести в нов разтвор подкрепа.

Правила за прехода към следната таблица:

видима индекс линия (последната) на таблицата и между коефициентите на линията (с изключение на колона на постоянни условия) се избира най-малкото отрицателно число в намирането на Стах, или най-положителните в решаване на проблема за минути. Ако има не е, тогава първоначалната основен решение е оптимално и тази таблица е късно;

Оценка колона на таблицата, съответстваща на избраното отрицателен (положителен) фактор в последния stroke- ключ колоната и тази колона са избрани положителни коефициенти. Ако няма такива, целевата функция е неограничено върху стойностите на толеранс на променливите и проблемът няма решение;

между избраната колона изберете коефициентите за която абсолютната стойност на съотношението на съответната свободна елемент (разположен в колона на членове) на елемента е минимална. Това съотношение се нарича толерантен и низ, в която е ключов;

допълнително основната променлива съответстващ толерантен клетъчна линия се прехвърля в изпускателния материал без променливата съответстващ толерантен колона елемент се въвежда в броя на основа. Изгражда нова таблица, съдържаща новите имена на основни променливи:

разделят всеки ключов елемент низ (с изключение на свободен членове колона), за да се даде възможност на елемент и получените стойности написани на реда с основна променлива нова симплекс таблицата променения.

Онлайн позволява разделена на елемент елемент и получената низ е писано в новата таблица на същото място.

нова таблица на всички елементи на ключовия колоната = 0, освен това позволява винаги е едно.

колона, която има ключова линия 0, в новата таблица няма да бъде същият.

линия, която има ключова колона 0, в новата таблица няма да бъде същият.

клетки, останали в новите маса съхранява резултат конверсия стари маса елементи: нов елемент е равна на възраст елемент минус фракция, числителя на която е продукт на текущия ред и позволяване елемент колона на ред резолюция елемент и текущата колона и знаменателят - позволява елемента.

Резултатът е нова симплекс таблица, съответстваща на новия основен решение.

Изчисляване Пример на метод симплекс

На втория лист на MS Excel работна книга получаваме решаването на проблема, използвайки идеите на симплекс - метод. Пишем на проблема в канонична форма. Намираме първата осъществимо решение. Системата е съвместима ограничение. Неговият ранг г = 4, по този начин броят на свободно променливи к = 6-4 = 2. Като свободен да избере x1 и x2, 0 ги приравняваме, това е, x1 = 0 и x2 = 0. Основни ценности на неизвестни, се изчислява от ограниченията на системата. Резултатите са показани на фигурата.

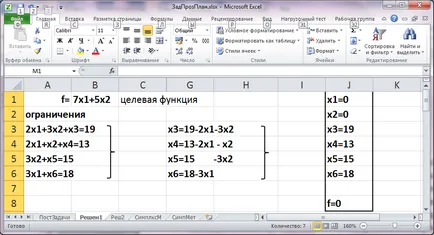
Първият валидно решение на проблема

Стойността на обективни резултати функция в решението е 0. анализира дали е възможно чрез промяна на x1 и x2 постигне повишена е. На записа целевата функция, която може да се дължи на увеличение на x1 или x2. Ние се увеличи x1 (x1 влиза в обективната функция с коефициент б lshim -7), докато наблюдават ограничения. От уравнение x3 = 19-2x1-3x2 следва, че x1 може да бъде увеличена до 19/2 = 9.5, уравнение х4 = 13-2x1 - х2 - 13/2 = 6.5, уравнението Х5 = 15-3x2 - 15/0 = ∞, уравнението X6 = 18-3x1- до 18/3 = 6. Избор на минимална стойност от 6 x1 и x6 превърнат в свободни променливи и x1 - основа. Ново изчисляване ограничение система от уравнения, експресиращи x6 = 18-3x1 x1 и се замести x1 = 6-1 / 3x6 други ограничения на уравнението на системата. Резултатът е показан на фиг.

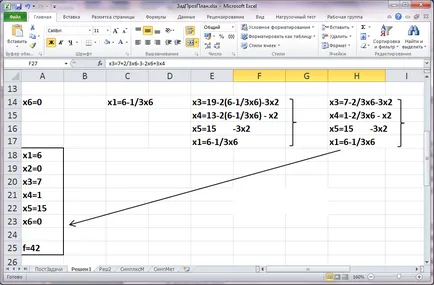
Изискан възможно решение на проблема

Новото решение е по-добре от предишната, тъй като стойността на целевата функция се е увеличил. Прилагането на идеята за симплекс - метод изпълнява последователност от две стъпки, за да се получи оптимално решение.

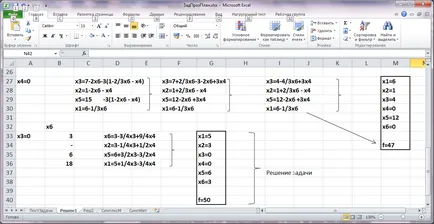
Третият лист реши проблема, в съответствие с обработката на симплекс - таблици. Симплекс - маса, съответстваща на първата допустима разтвора е показана на Фигура.

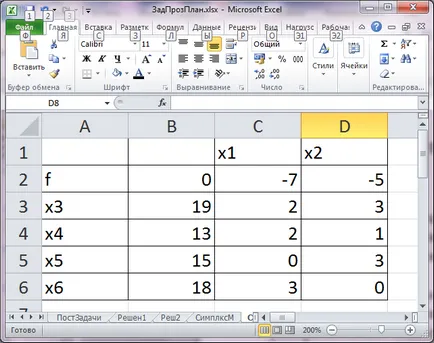
Първоначално Simplex - маса

Изберете Обща позиция - αsr. αsr = 3. Намираме  = 1 / αsr .Zanosim го в нова таблица в полето, съответстващо на общия елемент. Новата система на елементите, формиращи решаване на струните според правилото: да заема стойност от предходната таблица и се умножава по . Елементи, които позволяват броят на колона от правилото: стойността от предишния таблицата, умножена по -. Останалите клетки се напълват съгласно правилото: стойността на предходната таблица се изважда стойността на  на продукта от предходната таблица ред в резолюцията и текущата колона и стойността в предишния таблицата в текущия ред и колона толерантен. Последователно симплекс - таблица за изчисление е показано на фиг.

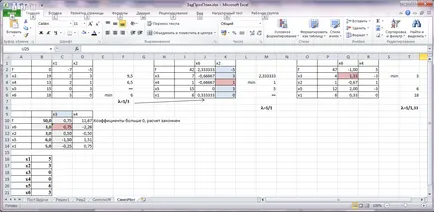
Решение с помощта на симплекс - маси

На четвърта страница на MS Excel работна книга доволни решение на проблема с помощта на "търсенето на решение."

Пълнене MS Excel лист клетки: