Изчисляване матрица метод ранг ресни непълнолетни

В предишната тема се разглежда концепцията за ранг на матрица, както и примери показват как да се намери в ранг по дефиниция. Разбира се, да се намери ранга на матрицата по този начин малко трудно - особено поради капацитета на компютри. Въпреки това, размерът изчислява непълнолетни могат да бъдат значително намалени чрез използване на така наречения метод на ресни непълнолетни.

Методът ресни малолетни и непълнолетни лица, изразено чифт точки прост алгоритъм:

Нека непълнолетен $ M $ к-ти, за да не е нула.
Ако ресни непълнолетни до незначително $ М $ (това е да непълнолетни (к + 1) -ти ред), за да направи възможно (например, матрицата съдържа к редове или к колони), равен на ранг к. Ако има навътре в непълнолетни лица и всички са равни на нула, а след това в ранг, равен на к. Ако сред малолетни и непълнолетни, граничещи да има поне една различна от нула, а след това повторете стъпка №1, като к + 1 вместо к за него.

Ясно е всичко по-горе може да се изрази със следната схема:

Изчисляване матрица метод ранг ресни непълнолетни

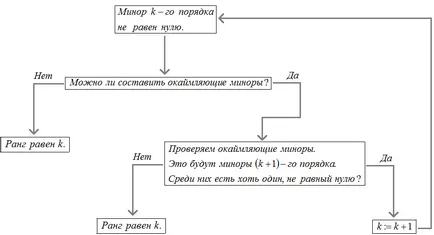
Ще обясня тази схема в по-големи подробности. Нека поговорим от самото начало, което е, малолетни и непълнолетни с първата поръчка. Ако всички от първия ред на някои непълнолетни матрица $ A $ (непълнолетни първи ред - елементите на матрицата) са нула, тогава $ \ позвъни А = 0 $. Ако матрицата е непълнолетния на първия ред $ M_1 \ НЕК 0 $, тогава $ \ звънна A≥ $ 1.

Проверете, граничещи на непълнолетни към второстепенен M_1 $ $. Това вече ще бъде непълнолетните от втори ред. Ако всички непълнолетни, граничещи M_1 $ $, равни на нула, а след това $ \ звънна = 1 $. Ако сред малолетни и непълнолетни лица от втори ред, граничещи M_1 $ $, има най-малко един Мала $ M_2 \ НЕК 0 $, тогава $ \ звъняха A≥ $ 2.

Проверете, граничещи на непълнолетни към второстепенен M_2 $ $. Това ще бъде непълнолетни от трети ред. Ако всички непълнолетни от третия ред, граничеща M_2 $ $, равни на нула, а след това $ \ звънна = 2 $. Ако сред непълнолетните от трети ред, граничещи M_2 $ $, има най-малко един Мала $ M_3 \ НЕК 0 $, тогава $ \ звънна A≥ $ 3.

Проверете, граничещи на непълнолетни към второстепенен M_3 $ $. Ако всички непълнолетни лица на четвърти ред ресни M_3 $ $, равни на нула, а след това $ \ звънна = 3 $. Ако сред непълнолетните на четвърти порядък, граничещи M_3 $ $, има най-малко един Мала $ M_4 \ НЕК 0 $, тогава $ \ звънна A≥ $ 4.

Проверяваме всички граничеща непълнолетните за дребни $ M_4 $, и така нататък. В крайна сметка, има две възможности: или на някакъв етап се оказва, че всички малолетни и непълнолетни лица са граничещи нула или непълнолетен ресни създават просто няма да работи, тъй като в матрицата "изчерпване" редове или колони. Редът на последния не е нула непълнолетния събере и ще бъде равен на ранга на матрицата.

Намери ранг на матрица $ A = \ ляв (\ започне -1 2 1 3 \\ -3 0 5 4 \\ -5 4 7 10 \ край \ вдясно) $ ресни от непълнолетни.

Можете, разбира се, започва с непълнолетните от първи ред, които са само елементи на матрицата. Но това е по-добре да се избере различен от нула непълнолетен на втория ред, толкова повече, така че този избор не е от голяма сложност. Така например, в пресечната точка на линиите №1, №2 и колони №1, №2 са елементи, дребни $ \ оставени | \ започне -1 2 \\ -3 0 \ край \ дясна | $, което е лесно да се изчисли, като се използва формулата №1 на нишките за изчисляването на детерминантите на втория и третия ред:

$$ \ лява | \ започне -1 2 \\ -3 0 \ край \ полето | = -1 \ cdot 0-2 \ cdot (-3) = 6. $$

Така че, има незначително от втори ред, различен от нула, което означава, че $ \ звънна A≥ $ 2. Разполагате с трети ред непълнолетни, съпътстващи активен непълнолетен втори ред. Напиши навътре в Мала? За тази цел, набор от редове и колони в пресечната точка на дребни елементи, които са от втори ред, ще трябва да добавите друг ред и друга колона. Запомняне че контактните елементи са записани малка втори ред се намират в пресечната точка на редове №1, №2 и колони №1, №2. Добавете повече редове в линията №3, а колоните - колона №3. Получаваме непълнолетен третия ред, чиито елементи (те са показани на фигурата в синьо) лъжа в пресечната точка на линиите №1, №2, №3 и колони №1, №2, №3.

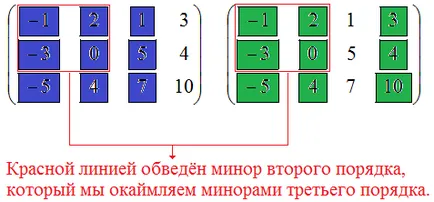
$$ \ лява | \ започне -1 2 1 \\ -3 0 5 \\ -5 4 7 \ край \ дясна | = 0. $$

Мала ресни нула. Какво означава това? Това предполага, че трябва да продължим да намери ресни непълнолетни. Или те са нула (тогава ранг е равен на 2), всеки един от тях има най-малко една нула.

Елементи на втория граничещи малка лежат в пресечната точка на линиите №1, №2, №3 и колони №1, №2, №4. Фигурата по-горе показва незначителни елементи на зелено. Изчисляваме непълнолетния, всички по същата формула, №2 на нишките за изчисляването на детерминантите на втория и третия ред:

$$ \ лява | \ започне -1 2 3 \\ -3 0 4 \\ -5 4 10 \ край \ дясна | = 0. $$

И това ресни Мала е нула. Други граничещи непълнолетни лица там. Следователно всички граничещи непълнолетните са равни на нула. Редът на последния не е нула непълнолетния се състои 2. Заключение: ранг е 2, т.е. $ \ Звънна = 2 $.

Намери ранг на матрица $ A = \ ляв (\ започне 1 2 0 4 5 \\ 3 6 -2 -1 -3 -2 \\ -4 2 5 7 \\ -1 -2 2 9 11 \ край \ вдясно) $ ресни от непълнолетни.

Отново, както в предишния пример, ние започваме с решението за избор на непълнолетен второ, за да не са равни на нула. Така например, в пресечната точка на линиите №1, №2 и колони №1, №2 са елементи, дребни $ \ оставени | \ започне 1 2 \\ 3 6 \ край \ дясна | $, което е лесно да се изчисли, като се използва формулата №1 на нишките за изчисляването на детерминантите на втория и третия ред:

$$ \ лява | \ започне 1 2 \\ 3 6 \ край \ дясна | = 1 \ cdot 6-2 \ cdot 3 = 0. $$

Мала активен втори ред нула, т.е. избор е неуспешен. Вземете малка втори ред. Например, елементите на които се намират в пресечната точка на редове №1, №2 и колони №2, №3:

По този начин, различен от нула непълнолетен втори ред там, така че $ \ звънна A≥ $ 2. Ще означаваме това като непълнолетен $ $ M_2 и стават кантиране своите непълнолетни лица от трети ред. Например, за да добавите редове и колони, в които има елементи на $ M_2 $ на, по линия №3 и колона №1. Т.е. намерите непълнолетен третия ред, чиито елементи са в пресечната точка на реда №1, №2, №3 и колони №1, №2, №3. Ние сме с помощта на формулата №2 на нишките за изчисляването на детерминантите на втория и третия поръчките. Подробни изчисления I водят не, запишете само отговора:

$$ \ лява | \ започне 1 2 0 \\ 3 6 \\ -2 -2 -4 2 \ край \ дясна | = 0. $$

Това Мала е нула, тогава ще трябва да се премести в друга Мала ресни. Или всички непълнолетните от третия ред, граничещи M_2 $ $, равни на нула, всеки един от тях все още има най-малко една нула.

Помислете за дребни елементи от трети ред са разположени в пресечната точка на линиите №1, №2, №3 и колони №2, №3, №4. Това Мала също граничи M_2 $ $:

$$ \ лява | \ започне 2 0 4 \\ 6 -2 -1 \\ -4 2 5 \ край \ дясна | = 0. $$

Отново непълнолетен трети ред ресни M_2 $ $, е равна на нула. Така че, ние се връщаме към друг второстепенен на третия ред. Вземете непълнолетен трети ред елементи лежат в пресечната точка на линиите №1, №2, №3 и колони №2, №3, №5. Това Мала също граничи M_2 $ $:

$$ \ лява | \ започне 2 0 5 \\ 6 -2 \\ -3 -4 2 7 \ край \ дясна | = 4. $$

Така сред непълнолетните от трети ред, граничещи M_2 $ $, има леко, различна от нула, което означава $ \ звънна A≥ $ 3. Ще означаваме това като не нулев непълнолетен M_3 $ $. Елементи на непълнолетен $ $ M_3 лъжата в точката на пресичане на линии №1, №2, №3 и колони №2, №3, №5. Станете кантиране Незначителни $ $ M_3 непълнолетни, четвърти ред. Да започнем с това ние се непълнолетен четвърти ред, чиито елементи лежат в пресечната точка на линиите №1, №2, №3, №4 и колони №1, №2, №3, №5. Това малки граници M_3 $ $. Неговата стойност не е трудно да се намери, ако използвате, например, разширяването на реда или колоната:

$$ \ лява | \ започне 1 2 0 5 \\ 3 6 -2 -3 -2 \\ -4 2 7 \\ -1 -2 2 11 \ край \ дясна | = 0. $$

По подобен начин, като се има предвид малка четвъртия ред, чиито елементи са разположени в пресечните точки на редове №1, №2, №3, №4 №2 и колони, №3, №4, №5, ние получаваме:

$$ \ лява | \ започне 2 0 4 5 \\ 6 -2 -1 \\ -3 -4 2 5 7 \\ -2 2 9 11 \ край \ дясна | = 0 $$.

Други, граничещи на непълнолетни към второстепенен $ $ M_3 не. Всички непълнолетни лица на четвърти ред ресни M_3 $ $, равна на нула. Последното не е нула непълнолетния, т.е. $ $ M_3, тя е три пъти. Заключение: чин е 3, т.е. $ \ Звънна = 3 $.

Намери ранг на матрица $ A = \ ляв (\ започне -1 3 2 4 1 \\ 0 -2 5 0 -3 \\ 1 -5 3 7 6 \ край \ вдясно) $ ресни от непълнолетни.

Отново, като се започне с решението за избор на непълнолетен второ, за да не са равни на нула. Така например, в пресечната точка на линиите №1, №2 и колони №1, №2 са елементи, дребни $ \ оставени | \ започне -1 3 \\ 0 -2 \ край \ дясна | $, която се изчислява по следната формула №1 на нишките за изчисляването на детерминантите на втория и третия ред:

Това Мала (означен с $ M_2 $) не е нула, следователно, че е това, което ние ставаме и кантиране на малолетни и непълнолетни лица от трети ред. Например, за да добавите редове и колони, в които има елементи M_2 $ $ и още ред №3 №3 колона. Т.е. намерите непълнолетен третия ред, елементите на които са разположени в пресечната точка на реда №1, №2, №3 и колони №1, №2, №3. Ние сме с помощта на формулата №2 на нишките за изчисляването на детерминантите на втория и третия ред:

$$ \ лява | \ започне -1 3 2 \\ 0 -2 5 \\ 1 -5 3 \ край \ дясна | = 0. $$

Помислете за дребни елементи от трети ред са разположени в пресечната точка на линиите №1, №2, №3 и колони №1, №2, №4. Това Мала също граничи M_2 $ $:

$$ \ лява | \ започне -1 3 4 \\ 0 -2 0 \\ 1 -5 7 \ край \ дясна | = 22. $$

Така сред непълнолетните от трети ред, граничещи M_2 $ $, има най-малко една нула. Непълнолетните форма четвърти ред вече не можем да, за техните нужда 4 линии, както и в матрицата $ A $ на всички 3 линии. Следователно, тъй като последната е различна от нула непълнолетен третия ред, ранг е 3, т.е. $ \ Звънна = 3 $.