Изчислителните стойности зона, ограничена от кривата даден параметрично

В изясняване на геометрична смисъла на определен интеграл. имаме формулата за намиране областта на криво трапец, ограничена от оста х. направо х = А, X = б и непрекъснат неотрицателна (не-положителна) функция у = е (х). В някои случаи, функция, която ограничава фигурата, удобно разположен в параметрична форма, т.е. осигури функционална връзка чрез параметър Т. В тази статия ще разгледаме как да се намери областта на фигурата в случай на ограничаване на крива параметричен работа.

След кратък преглед на теорията и извличането на формулата, считаме подробно решаването на типични примери за намиране на площта на фигурата, ограничена от параметрично дадена линия.

Навигация в страниците.

Формулата за изчисляване на площта на фигурата, ограничена от линия, посочено по параметри.

Нека границата на криволинеен трапец е директен х = а, х = б. абсциса и параметрично определена крива, и при което функции са непрекъснати на интервала, увеличава монотонно него и.

Тогава областта на криволинеен трапец се изчислява по формулата.

Тази формула е получена от формула квадратен заместване криволинейна трапец:

Ако функцията е монотонно намаляване на интервал, след това с формула става.

Ако функцията не е основният елементарното, а след това да се определи неговата възходящ или низходящ ред може да изисква от раздел теория на на увеличаване и намаляване функцията на интервал.

Примери за изчисляване на площта на фигурата, ограничена от предварително определена крива на параметри.

Да разгледаме примери за прилагането на формулата, получена, което позволява да се изчисли квадратни форми обградени параметрично определени линии.

Изчислява областта на фигурата, ограничена от линия, която има формата на параметрични уравнения.

В нашия пример, параметрично определена линия е елипса с полуоси 2 и 3 единици. Ние го изгради.

Намерете лицето на една четвърт елипса, намиращ се в първи квадрант. Тази област се намира в интервала. Площта на цялата фигура изчислява чрез умножаване на резултата по четири.

За к = 0 получаваме интервала. В този обхват, функция монотонно намалява (виж основните елементарни функции, техните свойства и графиките). Прилагането на формулата за изчисляване на района и определен интеграл от формулата основните теорема:

По този начин, първоначалната площ на фигурата е.

Налице е логичен въпрос: защо ние взехме една четвърт от елипса, а не наполовина? Можете да видите най-горния (или отдолу) половина на фигурата. Той се намира в интервала. За този случай, ние ще трябва

Това е, за к = 0 получаваме интервала. В този диапазон, а монотонно намаляваща функция.

След това половината от площта на елипсата е като

И тук е дясната или лявата половина на елипсата да вземе няма да работи.

Параметрични представяне на елипса с центъра на произхода и semiaxes А и В е дадено. Ако действието по същия начин, както в Пример разглобен се получи формула за изчисляване на областта на елипса.

Окръжност с център в основата на радиус R чрез параметър Т е дефинирано уравнения. Ако използваме площта на елипсата, получена по формулата, формулата може да се запише веднъж, за да се намери областта на окръжност с радиус R ..

Ние решаваме още един пример.

Изчислете площта на фигурата, ограничена от кривата е определено по параметри.

Работещи малко по-напред, кривата се "разтяга" astroid. (Astroid има следните параметри представяне).

Нека се спрем върху изграждането на формата на кривата очертаващ. Направете го, ние ще в точките. Обикновено такава конструкция е достатъчен за повечето цели. В по-сложни случаи, разбира се, това изисква подробно изследване на параметрично зададени функции, използващи диференциално смятане.

В нашия пример.

Тези функции са определени за всички валидни стойности на параметъра т. Освен това, свойствата на синус и косинус, ние знаем, че те са периодични с период от две пи. По този начин, чрез изчисляване на стойности за определени функции (например), ние получаваме набор от точки.

За удобство на стойностите, посочени в таблицата:

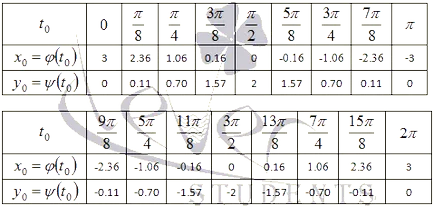
Отбелязваме точката на самолета и те са последователно свързани линия.

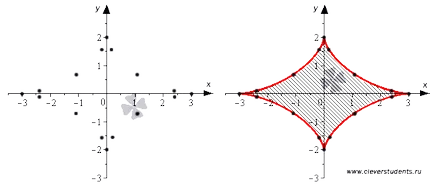
Изчисляваме областта на региона, разположен в първото тримесечие на координатната. За тази област.

За к = 0 получаваме интервала, на който функцията е монотонно намалява. Прилагането на формулата за намиране на района:

Определени интеграли получени с формула изчисляват основните теорема и примитивите на основните теорема с формула установено от рекурсия формула на формата, където.

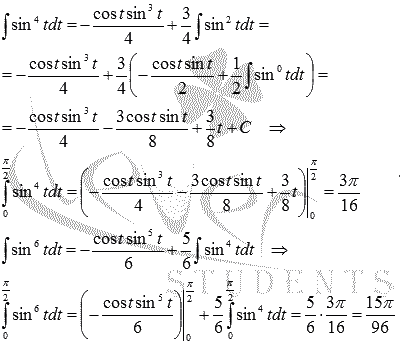
Следователно, районът е равна на една четвърт от тази цифра, след което площта на цялата фигура е.

Аналогично можем да покажем, че astroid района е като и област на фигурата, ограничена от кривата, изчислени с помощта на ур.