итерационни методи
С голям брой неизвестни на линеен системата уравнения Гаус схема на елиминиране, което дава точно решение, става доста трудно. В този случай, за да открие корените лесно да се използва приблизителни итерационни методи. Помислете за метода на повторение (метод Зайдел).
Като се има предвид система
Ако приемем, че диагоналните условия - коефициентите са различна от нула


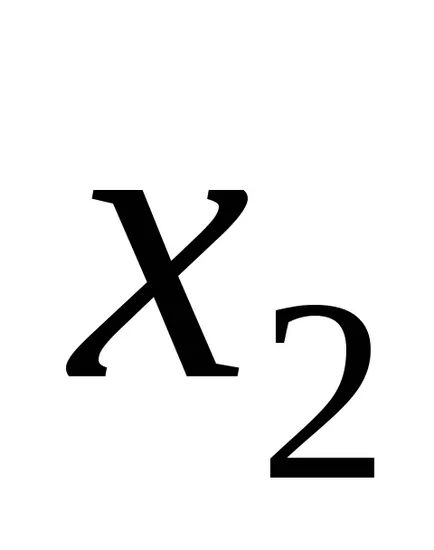
Системата (2) се постига чрез последователни приближения. Тъй като нула сближаване може да приеме всяка стойност. Често използвам това като колона на свободни условия.

Следващото сближаване се изчислява чрез заместване на стойностите
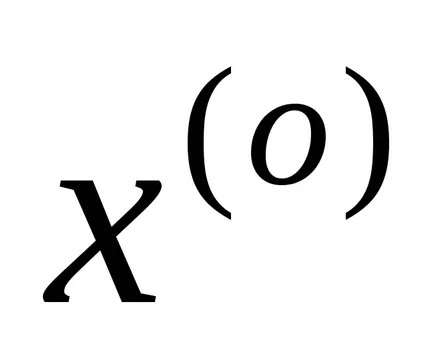
,
второ приближение се изчислява чрез първата:
.
Ако последователността на приближения


тази граница е разтвор на (2) и, следователно, на системата (1).
Пишем формулата приближения в разширена форма:
Методът на последователни приближения се определя с формула (3) се нарича с повторение. Итеративния процес клони добре, т.е. брой приближения, необходими за получаване на кореновата система (1) с определена точност е малък, ако елементите на матрицата

Да разгледаме система от линейни алгебрични уравнения с три неизвестни:
Ние избираме от дясната страна на всеки уравнение диагонал неизвестен
(Първоначална) Подходът на нула за решаване на някои от ценностите, които избират непознатото и да ги споделите

Системата (3) за изчисляване на неизвестното


Като цяло, в това повторение к- система тя изглежда така:
Това означава, че текущата стойност на неизвестното веднага се използва за последващи изчисления. Този метод се нарича повтарящ се начин на Гаус - Зайдел.


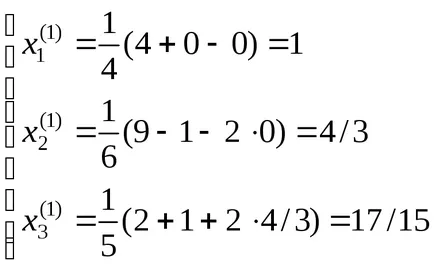
Точна разтвор търси от итеративния процес () ще бъде получено в 5-6-ти итерация.
В случай на система от уравнения н к - тата сближаване с решение би било:
Неколкократно процес продължава, докато всички

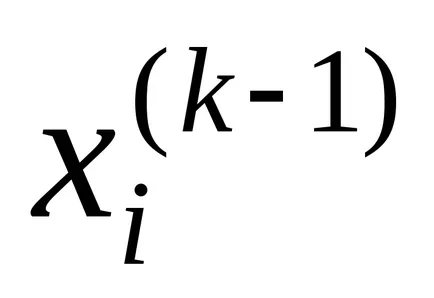
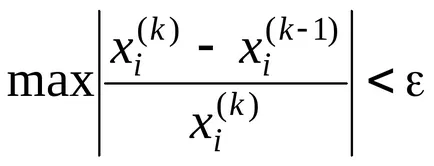
Помислете за начина на въпроси за конвергенция. Като се има предвид система от две уравнения на
,
От (1) и (3) получаваме
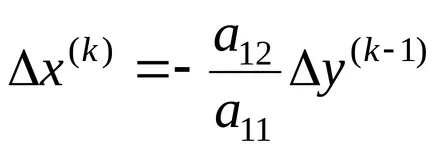

От последното уравнение следва:
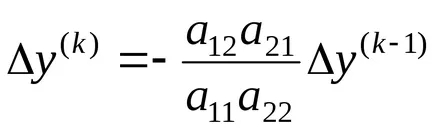
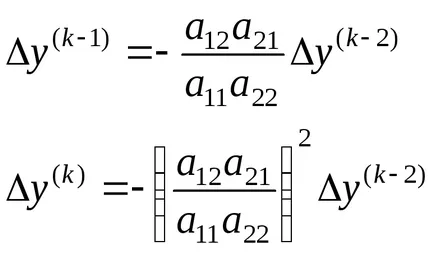
Продължавайки, можете да получите:

От това следва, че процеса на повторение на Гаус - Зайдел
клони, ако подходът към к- итерация ще се различава значително от първото сближаване. Това е възможно само при условие:

което означава, че диагоналните елементи на предимство пред останалите.
Предимството на метода на елиминиране е, че е ограничен и теоретично може да се използва за решаване на всеки не-дегенеративен система от линейни алгебрични уравнения. Повтарящ метод на Гаус-Зайдел клони само за специални системи от уравнения. Въпреки това, ако итеративен метод клони, за предпочитане е да:
време изчислителни
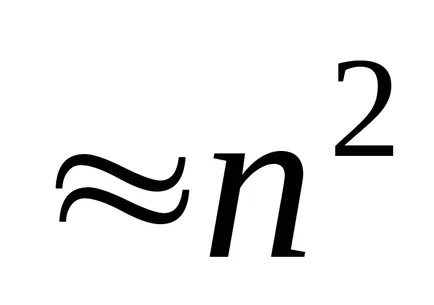

закръгляване грешка за итеративен метод по-малко.
големи системи от уравнения не могат да бъдат решени точно се използва прекия метод.