интегралите линията на първия вид
Да предположим, че кривата \ (С \) е описан от вектор функция \ (\ mathbf = \ mathbf \ наляво (S \ полето), \) \ (0 \ ле S \ ле S \) където променлива \ (и \) представлява дължината на дъгата крива (Фигура \ (1 \)).
Ако кривата \ (С \) се определя скаларна функция \ (F, \), а след това неразделна \ (\ вътр \ limits_0 ^ S \ ляв (и \ дясно)> \ вдясно) DS> \) се нарича линия неразделна от първи вид на скаларни функции \ (F \) по крива \ (с \) и е определен като \ [\ Int \ limits_C \ полето) DS> \; \; \; \ текстови \; \ ;. \ Int \ limits_C \] линията неразделна \ (\ Int \ limits_C \) съществува, ако функция \ (F \) е непрекъсната върху крива \ (с \)

Свойствата на линия неразделна от първи вид
Интегралната \ линия (I \) вид има следните свойства:Интеграл не зависи от ориентацията на кривата;
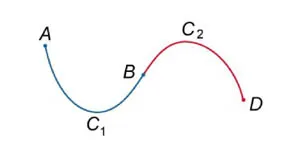
Да предположим, че кривата \ (\) започва в точка \ (А \) и завършва в точка \ (В, \) и крива \ (\) започва в точка \ (B \) и завършва в точка \ (Г \) (Фигура \ (2 \)). След комбиниране на тях ще се нарича крива \ (\ чаша, \), който се простира от \ (А \) на \ (B \) по крива \ (\) и след това от \ (B \) на \ (Г \) по крива \ за криволинейни интеграли на първия вид на връзка \ (\.) [\ Int \ limits_ \ чаша> = \ Int \ limits_> + \ Int \ limits_>; \]
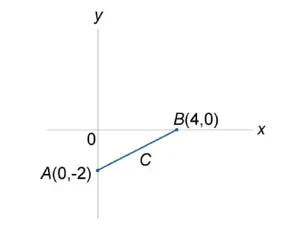
Виж неразделна \ (\ Int \ limits_C ярда> \) по линия сегмент \ на (у = х \) от произхода до точка \ (\ наляво (\ дясно) \) (Фигура \ (3 \)).


Изчислете неразделна \ (\ Int \ limits_C DS> \), където \ (С \) - дъга \ (х = а \ защото т \) \ (у = а \ грях т \) \ (0 \ ле т \ ле \ голям \ Фрак \ normalsize. \)
Изчислете неразделна \ (\ Int \ limits_C DS> \), където \ (С \) - кривата определя от уравнението \ (у = F \ наляво (х \ дясно) = \ LN х \) \ (1 \ ле х \ ле д. \)
Изчислете интеграл \ (\ Int \ limits_C \), където \ (С \) е отсечката от точка \ (О \ наляво (\ дясно) \) на \ (A \ наляво (\ дясно) \) (Фигура \ (4 \) по-горе).
Изчислете неразделна \ (\ Int \ limits_C +> \ дясно) ZDS> \) когато крива \ (С \) се определя параметрично като \ (\ mathbf \ наляво (т \ дясно) = \ наляво (\ полето), \) \ (0 \ ле т \ ле \ пи. \)
Изчислете линия неразделна \ (\ вътр \ limits_C >> \ normalsize> \), където кривата \ (С \) - отсечка от точка \ (\ ляво (\ вдясно) \) на \ (\ ляво (\ вдясно) \) (Фигура \ (5 \)).