Графичен метод за решаване на уравнения в Microsoft Excel 2018 среда
Вид на урока: Синтез, консолидиране на материала и обяснението на новото.
Цели и задачи на урока:
Оборудване, персонални компютри, мултимедиен проектор, прожекционен екран.
Материали за урока: Power Point презентация на компютъра на учителя (виж Приложение 1).
Плъзнете 1 от Prilozheniya1 (връзките към слайдовете отидат без Prilozheniya1).
1. Орална работа (актуализиране на знанията).
Slide 2 - отнасят следните функции с диаграмите на чертежа (Фигура 1.):
у = 6 - х; 2х + у = 3; у = (х + 3) 2; Y = - (х - 4) 2; ,
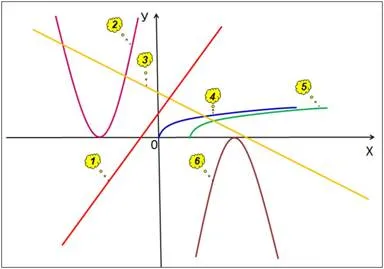
Слайд 3 графично разтвори на уравнения на F формата (X) = 0.
Корените на F в уравнение (х) = 0 са стойностите на x1. Х2, ..., генериран пропускателни пунктове на у = е (х) с хоризонтална ос (фиг. 2).

Виж корените на уравнението х 2 -2x-3 = 0. с помощта на графичен метод за решаване на уравненията (Фигура 3).

Slide 5 Графични метод разтвори на уравнения на форма F (х) = грам (х).
Корените на уравнение е (х) = грам (х) са стойностите на x1. x2, ... на пресечните точки на графики функция у = F (х) и у = г (х). (Фигура 4):
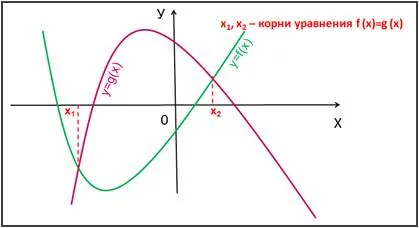
Slide 6 Виж корените на уравнението, с помощта на графичен метод за решаване на уравненията (фиг. 5).
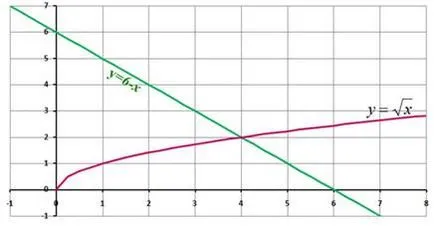
2. Обяснение на новия материал. Практическа работа.
I.Grafichesky начин за решаване на уравненията на F формата (X) = 0 в Excel.
По-нататъшната работа като учител в Excel в същото време с учениците, с подробни (ако е необходимо) инструкции и показва резултатите на прожекционен екран. Слайдовете допълнение 1 се използват за формулиране на цели и таблични междинни.
Пример 1: Използване на диаграми в Excel, графичен метод за решаване на уравнение 2 -x + 5x-4 = 0.
За тази диаграма на у функция = -x 2 + 5x-4 в интервала [0; 5] с нараствания от 0,25; \ Виж стойността на х на графиката на точките на пресичане с оста х.
А задача може да бъде разделен на етапи:
Етап 1: Въвеждане на функции в таблична форма (Фигура 6) .:
- в клетка A1 въведете текста в клетъчната H. А2 - Y;
- в клетка В1 въведете числото 0, клетъчната С1 - брой 0.25;
- подчертае клетки В1: С1. Преместете показалеца на мишката да се подчертае маркер, и момента, когато се променя мишката се черен кръст, за достигане на дясната дръжка избор да V1 на клетката (фиг. 7).
След въвеждане на клетката би формула изчисление резултат с формула и формула в областта на входния низ - самата формула (Фигура 8.):
- копиране на съдържанието на клетки В2 в клетка В2: V2 за селективния маркер. Цялата гама на избраните клетки, напълнени със съдържанието на първата клетка. В тази клетъчна позовавания в формули променят по отношение на отклонение самата формула.
Етап 2: изграждане на диаграми тип графика.
- изберете диапазона от клетки В2: V2;
- раздел Insert | Графика | Графика изберете вида на график;
- (. Фигура 9) | в раздела Проектиране Изберете данните в прозореца "Данни за избор на източник" кликнете върху бутона Edit в хоризонталните подписи ос - отваря прозорец "Подписи на оста." Разпределяне на група от клетки в Таблица В1: V1 (променлива х стойност). И в двата прозорци, като щракнете върху OK;

- в раздела Layout | Оси | Обобщение хоризонтална ос | Допълнителни параметри на основната хоризонталната ос, за да изберете:
Интервалът между маркировките 4;
Интервалът между подписи на: Единична интервал: 4;
Регламент ос на отделения;
Изберете ширината и цвета на линия (разделите тип линия и цвят линия) на;
- независимо промените ширината и цвета на линията за вертикалната ос;
- В раздела Layout | Grid | вертикални решетъчни линии на главната ос, за да изберете от основните линии на мрежата.
Един примерен резултат операция е показано на фиг. 10:

Стъпка 3: Определяне на корените на уравнението.
Графиката на у = -x 2 + 5x-4 пресича оста х в две точки и поради това уравнение 2 -x + 5x 4 = 0 има две корени: Х1 = 1; х2 = 4.
II. Графичният метод за решаване на уравненията на форма F (х) = грам (х) в Excel.
Пример 2: решаване на уравнение графично.
За тази цел в една координатна система за парцел функции и Y1 = Y2 = 1-х в интервала [1; 4] с нараствания от 0,25; намиране на стойността на х е пресечната точка на графики на функции.
Етап 1: Въвеждане на функции в таблична форма (Фигура 1.)
- Отиди на Sheet2.
- Както в пример 1. При копиране на техники, попълнете в таблицата. Когато табулиране функция y1 = използва вграден в основата (фиг. 11).
Етап 2: изграждане на диаграми тип графика.
Един примерен резултат операция е показано на фиг. 12:
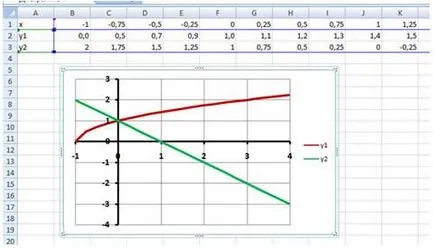
Стъпка 3: Определяне на корените на уравнението.
Графики функции Y1 и Y2 = 1-х = пресичат в една точка (0, 1) и следователно, уравнението има един корен - абсцисата на точката х = 0.
III.Metod Плуто.
Графичен метод за решаване на уравнения е красива, но не винаги в точката на пресичане може да бъде толкова "добра", в специално подбрани примери 1 и 2.
Възможности за електронни таблици дават възможност да намерите приблизителните стойности на конете на уравнението с определена точност. За да направите това, използвайте параметъра за избор на начин.
ПРИМЕР 3 Нека разгледаме метод за избиране на параметрите на например разтвори на уравнението 2 -x + 5x-3 = 0.
Етап 1: Изграждане на диаграми тип графика за приблизителното определяне на корените на уравнението.
Начертава се функция Y = -x 2 + 5x-3. редактирането, получен в пример 1, с формула.
- кликнете два пъти върху клетка В2. направи необходимите промени;
- използване на селективния маркер копиране формула във всички клетки диапазон С2: V2.
Всички промени са веднага показани на графиката.
Един примерен резултат операция е показано на фиг. 13:

Етап 2: Определяне на приблизителни стойности на корените на уравнението.
Графиката на у = -x 2 + 5x-3 пресича хоризонталната ос в две точки и следователно уравнението 2 -x + 5x 4 = 0 има две корени.
Според графика можем да определите приблизителната че x1 ≈0,7; x2 ≈4,3.
Стъпка 3: Намерете приблизителна решение на дадена точност от Удовлетворяване.
1) Започнете с търсенето на по-точна стойност по-малка корен.
От графиката се вижда, че аргумента с точност до пресечната точка на графиката с хоризонталната ос е 0.75. Стойностите на таблицата на функция, този аргумент се поставят в клетка Е1.
- Изберете клетка E2;
- Отидете в раздела Данни | Анализ на "какво-ако» | Удовлетворяване ...;
В диалогов параметър за избор на клетка. (Фигура 14) в областта на стойността, която влиза желаната стойност на функцията: 0.
В променящата се стойност на клетката. въведете $ E $ 1 (кликнете върху клетка E1).
Щракнете върху бутона OK.
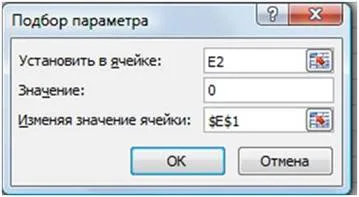
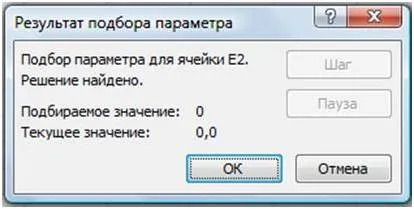
- (. Фигура 15) в резултат на селекцията показва информация за избраната стойност и съответства на стойностите на:
- Изходният Е1 клетката избран 0.6972 аргумент стойност с желаната точност (0.0001).
Настройване на точността може да се постигне чрез инсталиране в клетките на маса точно представяне на различните числа - броят на знака след десетичната запетая (Format Cells | Брой | Цифров).
Така че, първият корен на уравнението се определя с определена точност: x1 ≈0,6972.
2) намери своя стойност по-голяма коренова със същата точност. (X2 ≈4,3029).
IV.Metod параметър за избор на решенията на уравнения на форма F (х) = грам (х).
При използване на метода за избор на параметри за решаване на уравненията на форма F (х) = грам (X) се въвежда допълнителна функция у (х) = е (х) -G (х) и да намерят необходимата точност на стойност X на графиката на пресечните точки у (х) абсцисата.
3. Ремонт на материала учи. Независима работа.
Задача: Като се използва методът на подбор на параметри, за да открие корените на до 0001.
- въведете функция Y = и изграждане си графика на интервала [1; 4] с нараствания от 0.25 (фигура 16.):

- намери приблизителна стойност на х на графиката на точките на пресичане с абсцисата (х ≈1,4);
- намери приблизително разтвор до 0001 от параметър за избор (х ≈1,438).
Плъзнете 12 Резултатите от тестовете на самостоятелна работа.
Slide 13 Повтаряне на процеса графичните решения формата на F в уравнение (х) = 0.
Slide 14 Повтаряне на процеса графичните решения форма на уравнението F (х) = грам (х).
5. Домашна работа.
Използване на диаграми в Excel и параметър за избор метод определя корените на -5Н х 2 + 2 = 0 до 0,01.