Графичен метод за решаване на линейни програмни проблеми при използването на електронни таблици в Excel

Изявление на проблема
Намерете най-графичен метод максимума на целевата функция

Решение с помощта на електронни таблици
Най-напред се изгради Excel лист разтвор на неравенството на.
Помислете за първото неравенство.
Ние изграждане на граничната линия на две точки. Означава един с права (L1) (или Series1). Координати x2 помисли по следните формули:

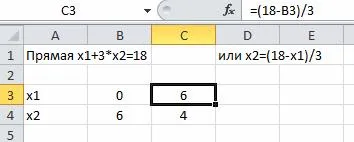
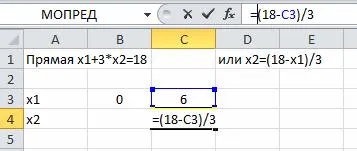
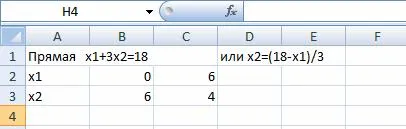
За да се построи изберете точкова диаграма

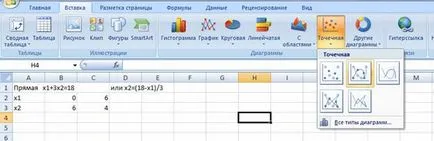
Избор на данни за

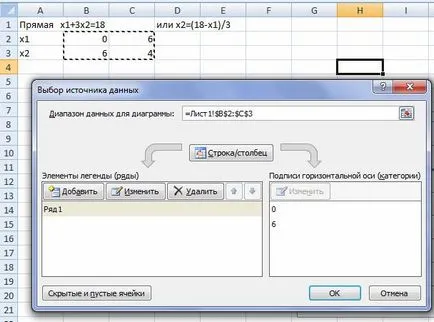
Промяна на името на правата линия:

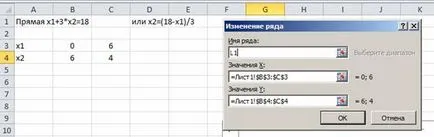
Изберете оформлението на графиката. Промяна на името на координатните оси:


Direct (L1) на графиката:

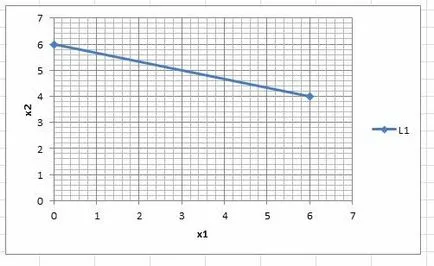
Решение строго неравенство може да се намери с една точка тест не принадлежи на пряката (L1). Например, с точка (0, 0)Ï(L1).
Чрез заместване на координатите на точка (0, 0), получаваме
0 + 3 х 0 <18 или 0 <18.
В неравенството е вярно, следователно разтвор на (1) ще бъде половината равнината, в която се намира точката за вземане на проби (показано по-долу на линия L1).
След решаване неравенството (2).
Ние изграждане на граничната линия 2 в две точки. Означава един с права (L2).

Direct (L2) на графиката:

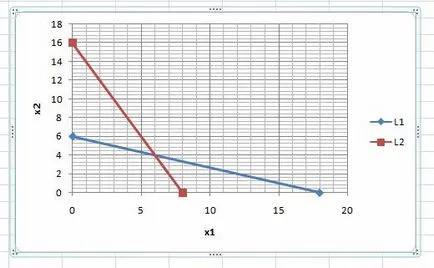
Решение строго неравенство 2 може да се намери с една точка тест не принадлежи на пряката (L2). Например, с точка (0, 0)Ï(L2).
Чрез заместване на координатите на точка (0, 0), получаваме
2 х 0 + 0 <16 или 0 <16.
В неравенството е вярно, следователно разтвор на (2) ще бъде половината равнината, в която се намира точката за вземане на проби (на фигурата по-долу правата линия L2).
След решаване неравенството (3).
Ние изграждане на граничната линия на две точки. Означава един с права (L3).
В работния лист Excel, за да добавите данни


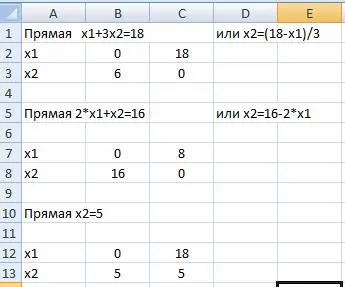
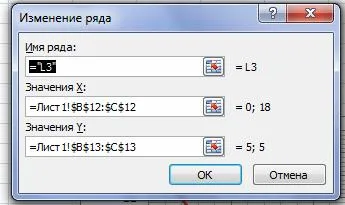
Директен (L3) в графиката:

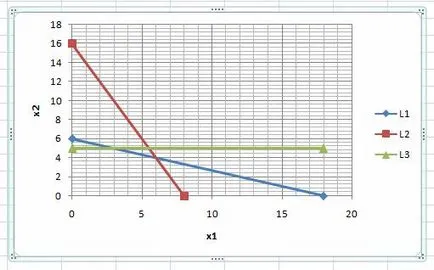
Решение строго неравенство 2 може да се намери с една точка за вземане на проби не е собственост, пряко (L3). Например, с точка (0, 0)Ï(L3).
Чрез заместване на координатите на точка (0, 0), получаваме
0 <5.
В неравенството е вярно, следователно разтвор на (3) ще бъде половината равнината, в която се намира точката за вземане на проби (показано по-долу на линия L3).
След решаване неравенството (4).
Ние изграждане на граничната линия на две точки. Означава един с права (L4).
В работния лист Excel, за да добавите данни


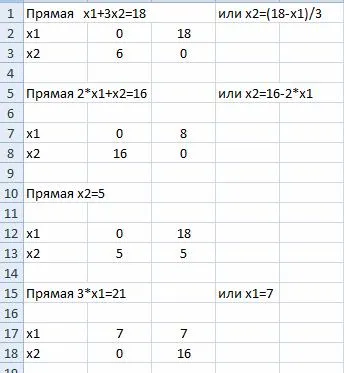
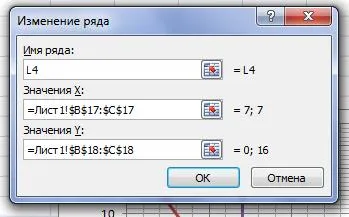
Direct (L4) в диаграмата:

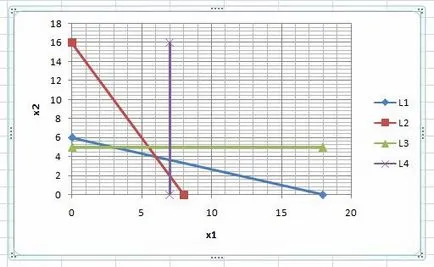
Решение строго неравенство 3x1 <21 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L4). Например, с помощью точки (0; 0)Ï(L4).
Чрез заместване на координатите на точка (0, 0), получаваме
0 <21.
В неравенството е вярно, следователно разтвор на (4) ще бъде половината равнината, в която се намира точката за вземане на проби (на фигурата отляво на линията L4).
Решение две неравенства (5) и (6)
и
Това е първото тримесечие, се ограничава прякото и координира.
система на неравенството е решен. Решение на системата от неравенства (1) - (6) в този пример е изпъкнал многоъгълник в долния ляв ъгъл на фигурата, ограничена от правите линии, L1, L2, L3, L4 и преки и координират. Уверете се, че полигонът е избран правилно, може да бъде замяната на точка на съдебен процес, например, (1, 1) във всяка неравенство на оригиналната система. При заместване на точката (1; 1), че всички неравенства, включително природни ограничения са верни.
Нека сега разгледаме целевата функция
F = 2x1 + 3x2.
Построява крива ниво на стойности на функцията F = 0 и F = 12 (числени стойности са избрани на случаен принцип). В работния лист Excel, за да добавите данни

ниво линия в графиката:

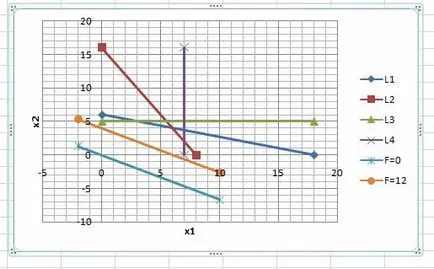
Изграждане на вектор посоки (или градиент). векторни координати съвпадат с коефициентите на обективната функция F.
Като прибавим към Excel лист координати на началната и крайна точка вектор.

Vector по-долу:

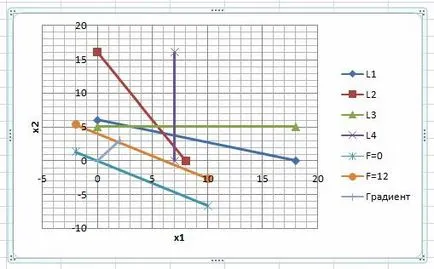
Градиентът показва посоката на увеличаване на целевата функция F.
Сега следва кривата на ниво F = 0 ход в паралел до последната точка на ъгловите точки на изпъкнал многоъгълник. Последният ъгъл точката на пресичане на изпъкнал многоъгълник, а се движи линията на ниво ще бъде точката на пресичане на линиите L1 и L2. За да намерите координатите на точката, решаване на системата уравнения

2
Ние се реши системата уравнения от правилото на Креймър. За да направите това в работен лист на Excel, за да създадете масиви от детерминанти. За изчисляване на детерминанти с помощта на математическа функция MDETERM

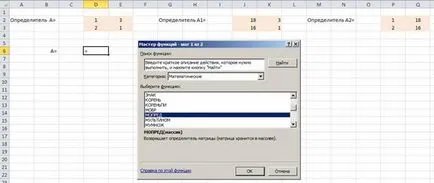
Изберете определящ фактор на масив



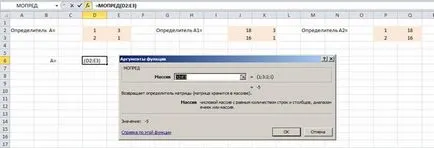
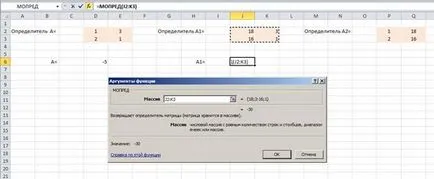
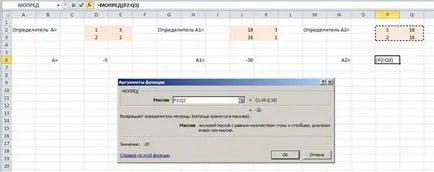
Ние намираме стойностите на x1 и x2



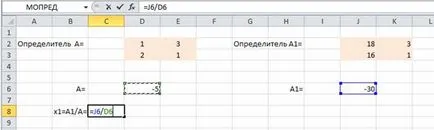
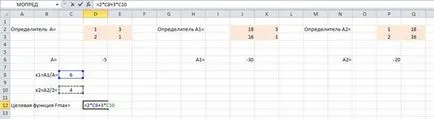
Пресечната точка на линии L1 и L2 ще бъде точка с координатите (6, 4).
Замести координатите на целевата функция
Fmax = 2 х 6 + 3 х 4 = 24
Отговорът е: Fmax = 24 и под.

влизане Правила данни

Задайте своите въпроси или да направите предложения или коментари могат да бъдат долната част на страницата в раздела Disqus.
Можете също така да изпратите заявка за помощ при справянето с изследвания на наши доверени партньори (тук или тук).